目录
在过去的两年里, ChatGPT 和大型语言模型 (LLM) 总体上一直是人工智能领域的大事。已经发表了许多关于如何使用、提示工程和背后的逻辑的文章。尽管如此, 当我开始熟悉 LLM 的算法(所谓的 transformer)时, 我必须浏览许多不同的来源才能感觉自己真正理解了这个主题。
1. Transformers的概念
1.1 Transformer简介
如果不引用 Vaswani 等人在 2017 年发表的著名论文"Attention Is All You Need", 我们就无法讨论大型语言模型的话题。在本文中, 一组研究人员介绍了引发我们今天经历的生成式 AI 革命的注意力机制和转换器架构。最初, 该论文提到了机器语言翻译, 并引入了编码器-解码器结构。
相比之下, ChatGPT 具有仅限解码器的架构。因此, 在下文中, 我们将忽略左侧, 完全专注于解码器。
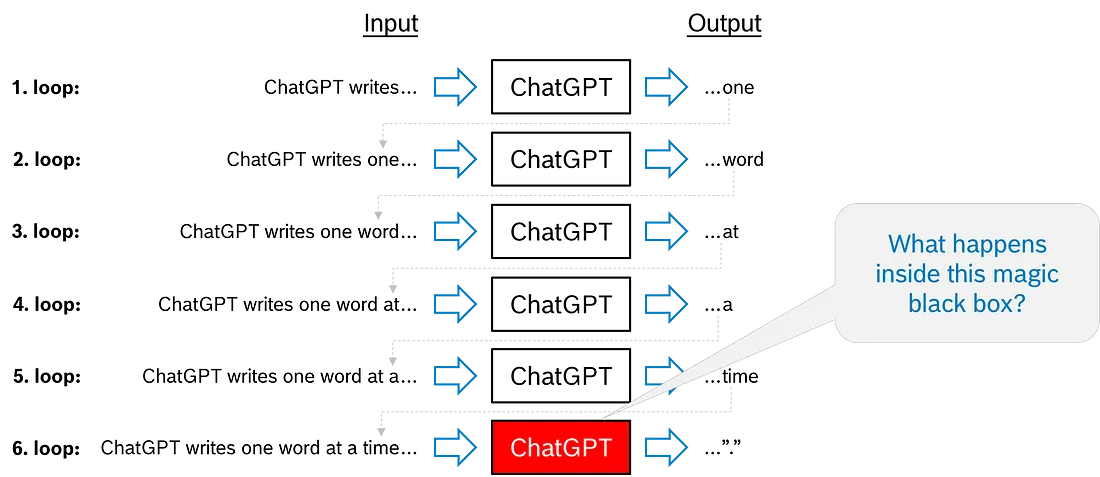
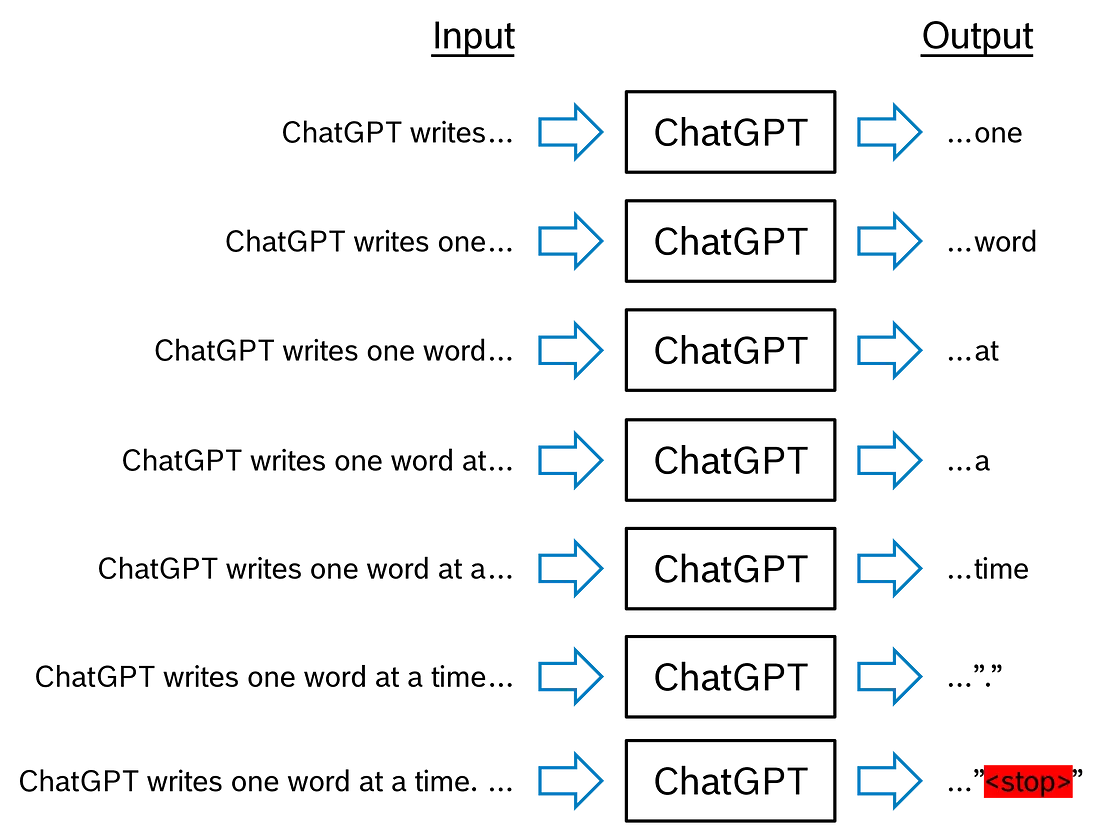
ChatGPT 在一个循环中生成其输出, 一个接一个。假设我们输入了"ChatGPT writes…“这几个字。(是的, 我知道这个上下文不切实际地简短)。ChatGPT 可能会输出令牌”…one"。初始单词加上第一个输出为第二代周期构建了上下文, 因此输入是 “ChatGPT writes one…"。现在, ChatGPT 可能会输出”……word", 该上下文将连接到现有上下文并再次输入。此循环一直持续到生成的输出是停止令牌, 这表示响应已结束, 并且生成循环结束, 直到下一次用户交互。
ChatGPT 中使用的 Transformer 架构
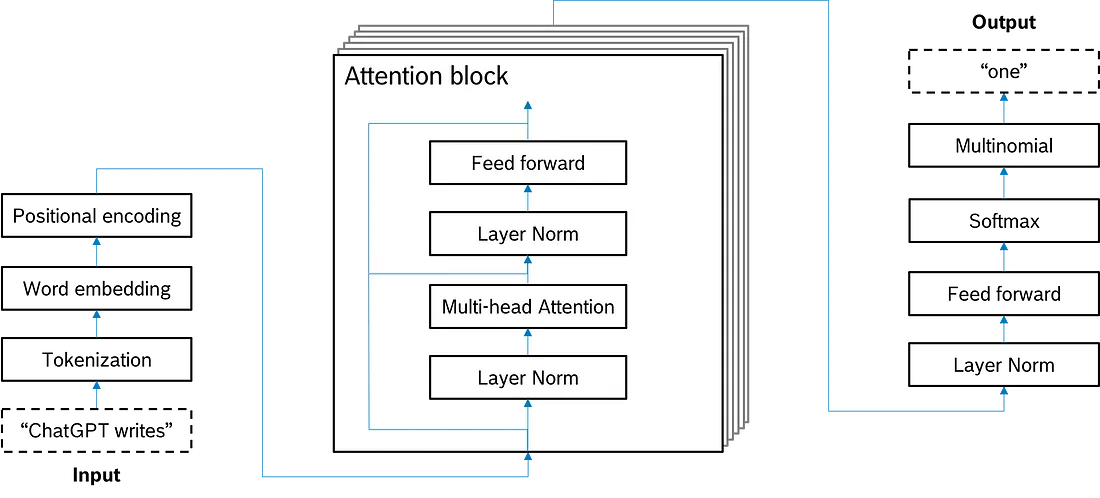
在图中, 我们看到左下角的变压器输入——词元序列 “ChatGPT writes…” —— 以及右上角的变压器输出, 即 “…one”。输入和输出之间会发生什么变化?
1.2 分词
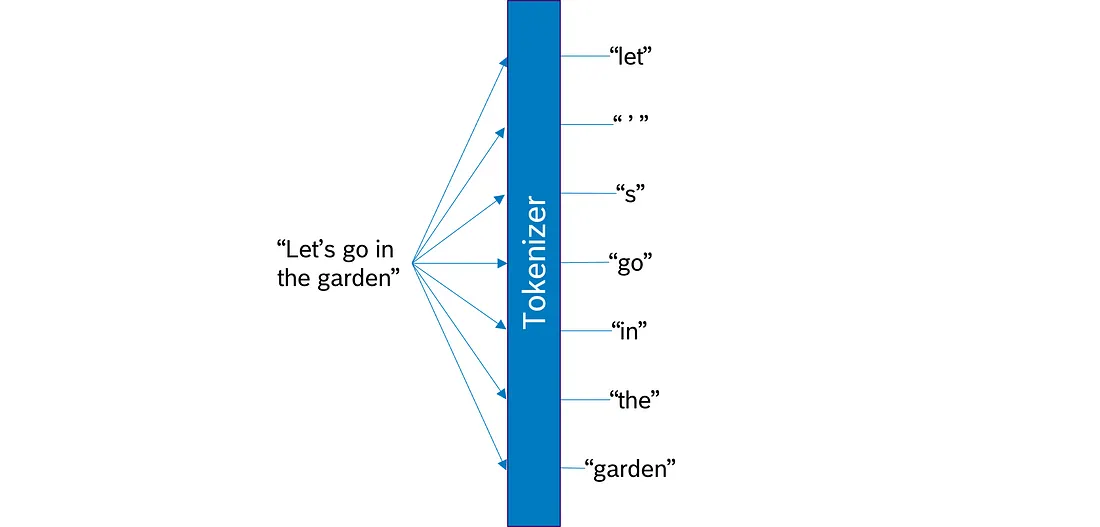
标记是大型语言模型中文本处理的基本构建块。将文本拆分为标记的过程称为标记化。根据令牌化模型, 收到的令牌看起来可能大不相同。一些模型将文本拆分为单词, 另一些模型拆分为子词或字符。无论粒度如何, 分词模型还包括标点符号和特殊分词, 如
分词的基本思想是将处理后的文本拆分为 LLM 知道的可能很大但数量有限的分词。
1.3 单词嵌入
嵌入将标记转换为通常具有数百或数千个维度的大型向量, 具体取决于所选模型。通常, 嵌入深度越高(意味着向量越大), 嵌入可以捕获的信息就越多。
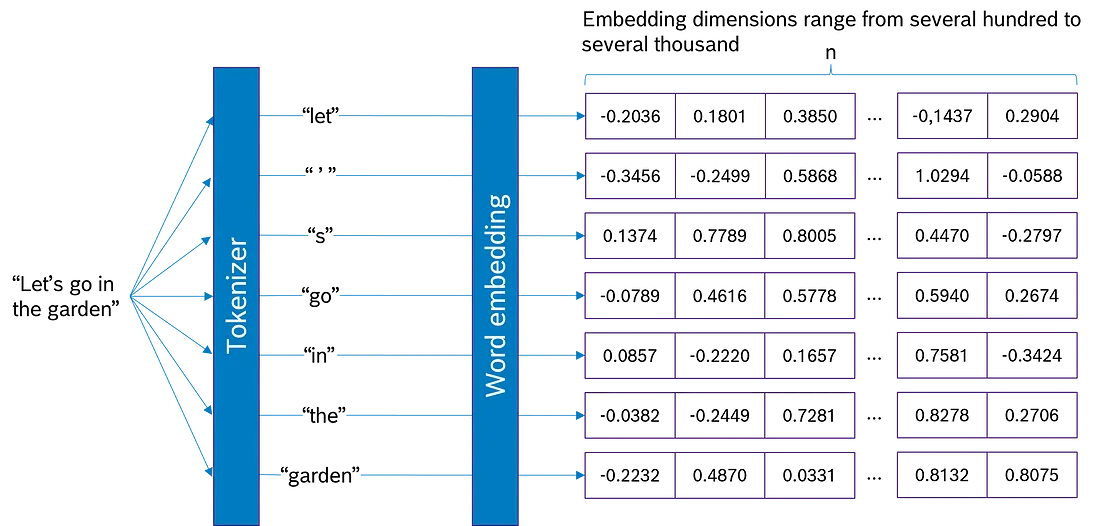
单词嵌入的有趣之处在于它捕获了标记的特征。其中一个含义是, 具有相似含义的单词获得相似的单词嵌入, 因此位于嵌入空间的附近。标记的这一特征会在嵌入过程中自动捕获, 因为具有相似含义的单词在相似的上下文中使用。
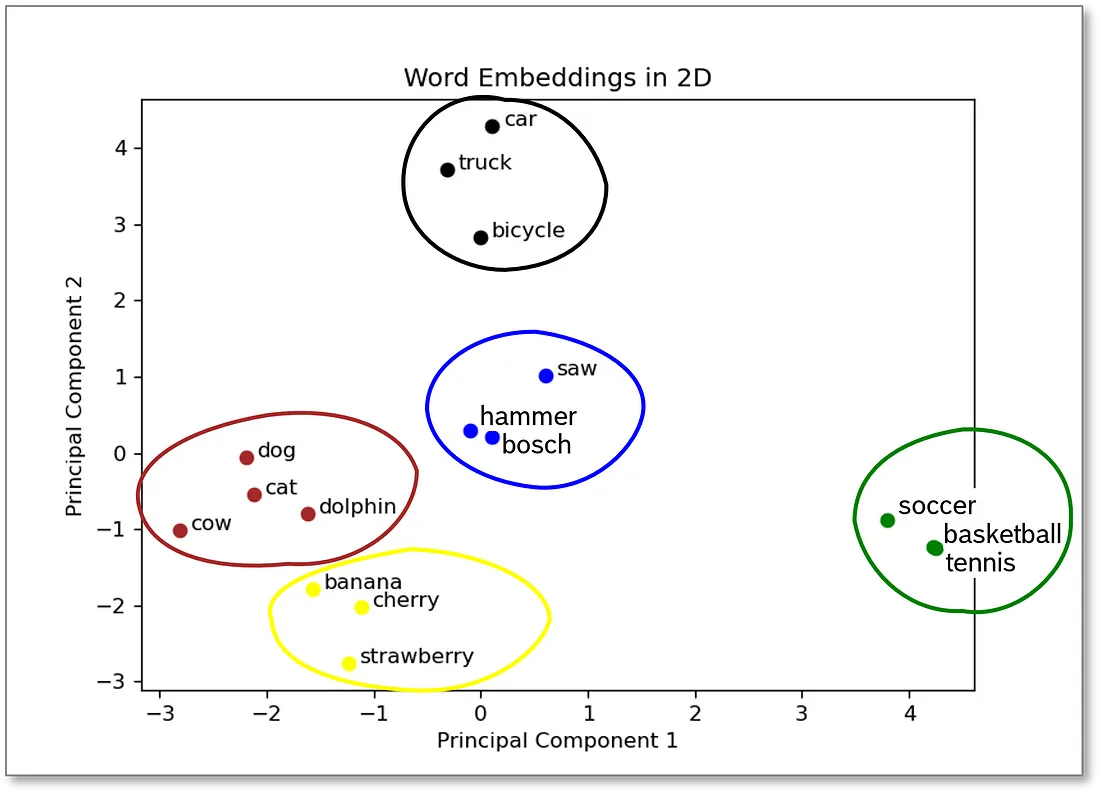
在图中, 你会看到原始嵌入深度为 100 的示例单词。为了在平面中绘制嵌入向量, 我使用主成分分析 (PCA) 将嵌入向量减少到 2 维。我们看到, 描述动物的词语会形成一个集群, 水果会形成另一个集群, 工具、车辆和运动也是如此。因此, 具有相似含义的单词位于附近, 因为它们具有相似的嵌入。
单词嵌入方法各不相同。这里勾勒的方法只是一种方法。

单词嵌入来自 Encoder-Decoder 神经网络。这种架构的典型情况是将输入压缩到较低的维度, 然后我们尝试从那里将信息重构到更高的维度。在图中, 我们在第一层和最后一层的词汇表中每个词元都有一个节点。我们将一个或几个单词输入编码器, 在相应的节点中为 “1”, 在所有其他节点中为 “0” (one-hot encoding)。网络将信息压缩到一个较低的维度——等于嵌入深度——并从那里尝试完成一项任务, 例如预测序列中的下一个单词。如果计算的输出错误, 则通过反向传播更新模型的权重。一旦我们达到足够的准确率, 我们就将较低维度的权重作为我们的词嵌入。
1.4 位置编码
单词嵌入不跟踪单词顺序。句子 “Today, I’m not happy, I am sad!” 与句子 “Today, I’m not sad, I am happy!” 获得完全相同的嵌入向量。当然, 作为人类, 我们知道这两种说法都有相反的含义, 但 transformer 没有!
这就是位置编码发挥作用的地方。主要思想是向每个嵌入向量添加一个与单词嵌入相同大小的向量。位置向量指定标记在上下文中的位置。
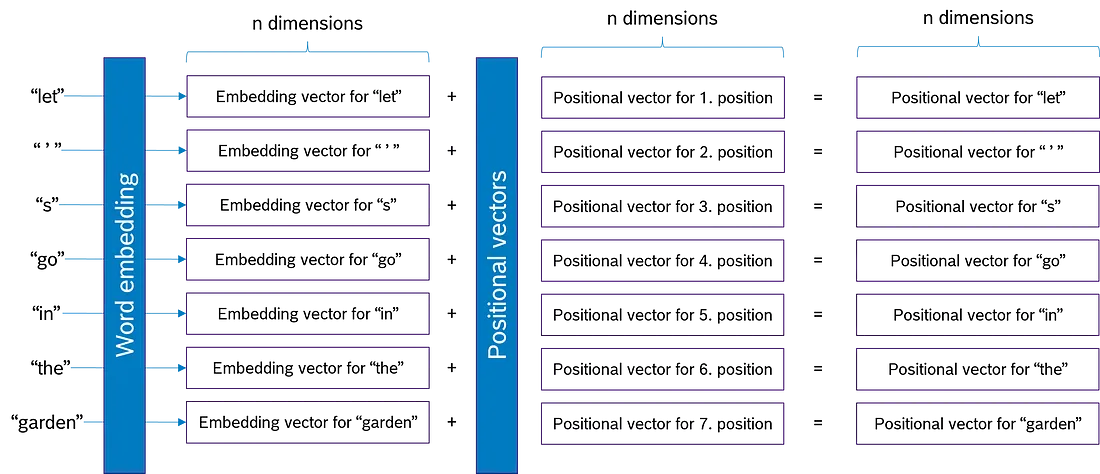
图延续了我们的 “Let’s go in the garden” 的例子。我们看到, 对于这七个词元中的每一个, 都添加了一个大小相等 n 的位置向量。位置向量编码 1st、2nd、3rd,…position 的 Context。因此, 嵌入向量和位置向量之和包含有关标记及其位置的信息, 并且不再独立于词序。使用位置编码时, “I’m not happy, I am sad!“和"I’m not sad, I am happy!“的嵌入向量不再相等!
何确定位置向量呢?事实上, 有不同的方法, 我只介绍其中的两种:
- “Attention is all you need"中描述的方法
- 本文编码中使用的一种简化方法。
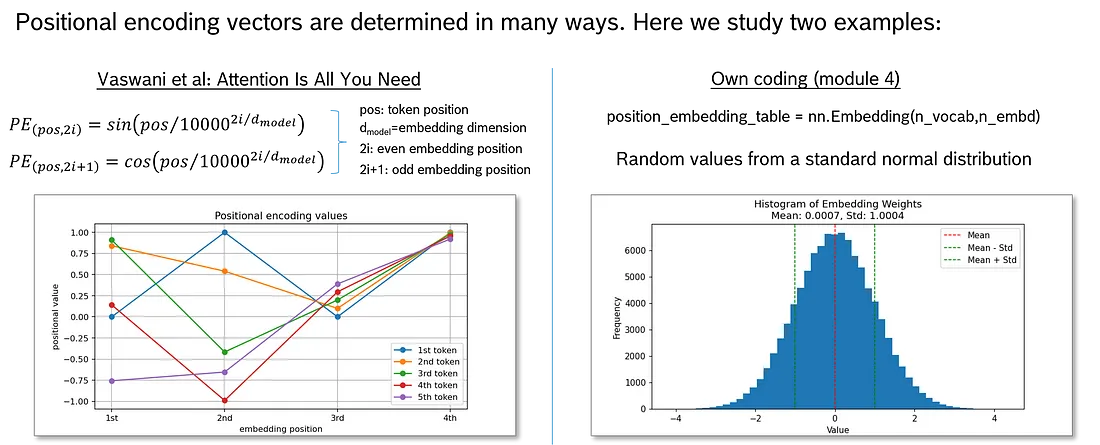
Vaswani 等人建议使用正弦和余弦函数来确定位置向量(图左)。“pos” 代表上下文中的令牌位置: 第一个令牌、第二个令牌、第三个令牌……2i 和 2i+1 表示奇数和偶数嵌入位置(位置向量内的位置)。I 从 0 运行到 dmodel/2。对于偶数嵌入位置, 本文使用 sine 函数, 对于奇数嵌入位置, 本文使用余弦函数。使用 PyTorch 嵌入模块, 该模块初始化为标准的法态分布值。这意味着只确定位置向量的大小, 但向量值是随机的。当然, 一旦确定, 就会保留 1st、2nd、3 的位置向量,…position 在 LLM 的整个生命周期中固定。
个人的印象是, 位置矢量的计算方式对于 transformer 的性能不太重要。但是, 无论矢量是如何计算的, 使用位置编码都至关重要。
1.5 注意力机制
注意力机制是变压器的心脏。这是 ChatGPT 如此擅长语言处理的主要原因。
1.5.1 根据上下文调整单词嵌入
在人类语言中, 单词和句子的上下文对于理解它们的含义非常重要。单词在不同的上下文中可能具有不同的含义。
词嵌入已经考虑了哪些词更频繁地与其他词相关联。但是单词嵌入不考虑特定情况下的上下文。我们可以说单词嵌入具有静态上下文, 而我们需要一个动态上下文, 该上下文在其特定的逻辑设置中考虑特定句子。
单词在不同的上下文中可以具有不同的含义
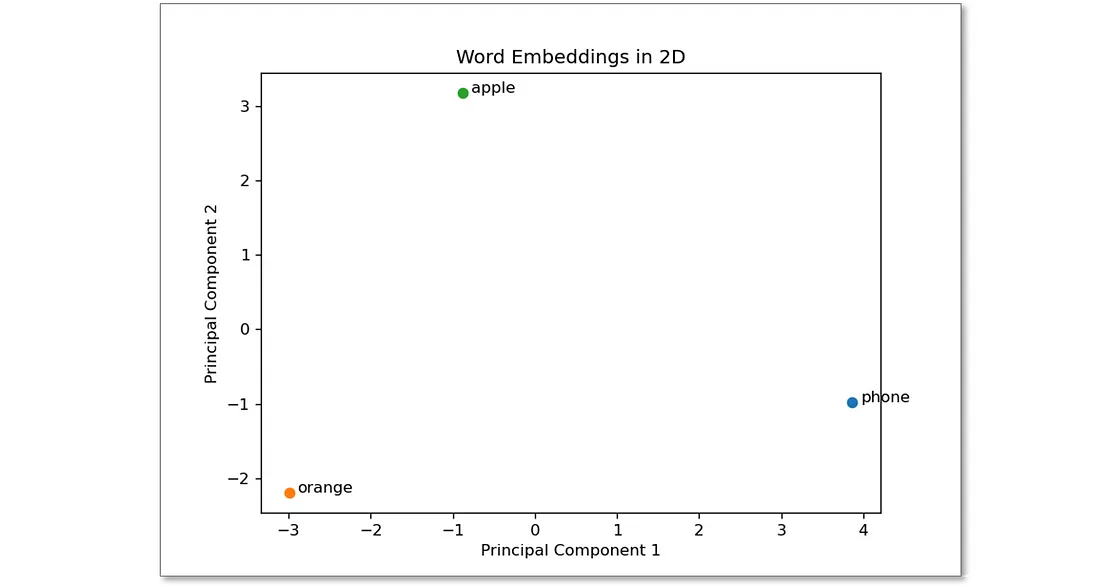
图显示了我们从 GloVe 中得到的单词 embedding。如您所见, “apple” 一词既不靠近 “phone” 一词, 也不靠近 “orange” 一词。
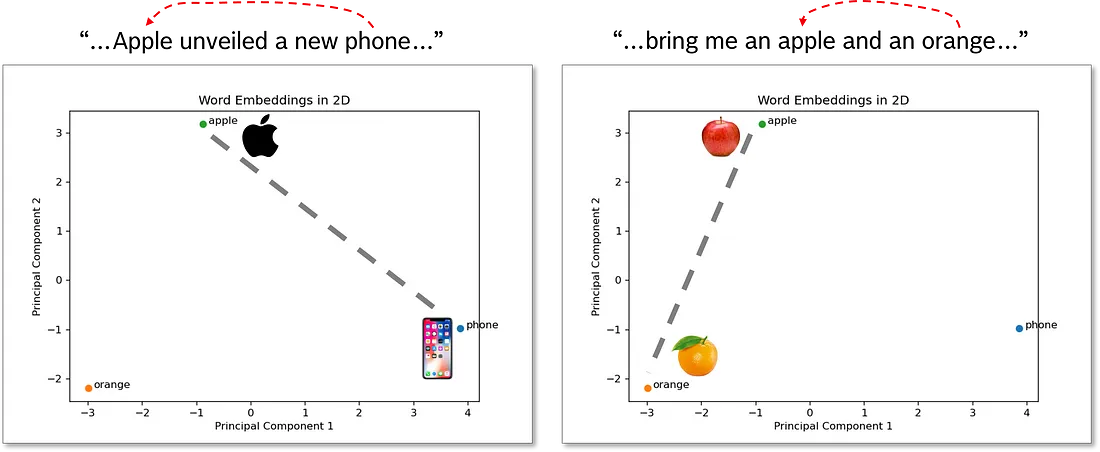
现在, 想象一下我们想要嵌入句子 “apple unveiled a new phone”。作为人类, 我们立即知道"apple"这个词代表科技公司。我们怎么知道的?具体的上下文告诉我们, 特别是 “phone” 这个词。
接下来, 假设我们想要嵌入句子 “bring me an apple and an orange”。同样, 作为人类, 我们立即知道这一次我们谈论的是水果。特别是"orange"这个词非常有用。
如何教计算机理解上下文?这就是注意力机制的意义所在!attention 的核心思想是在非常具体的上下文中修改单词嵌入。因此, 我们将单词移近嵌入空间中具有上下文关系的那些单词。
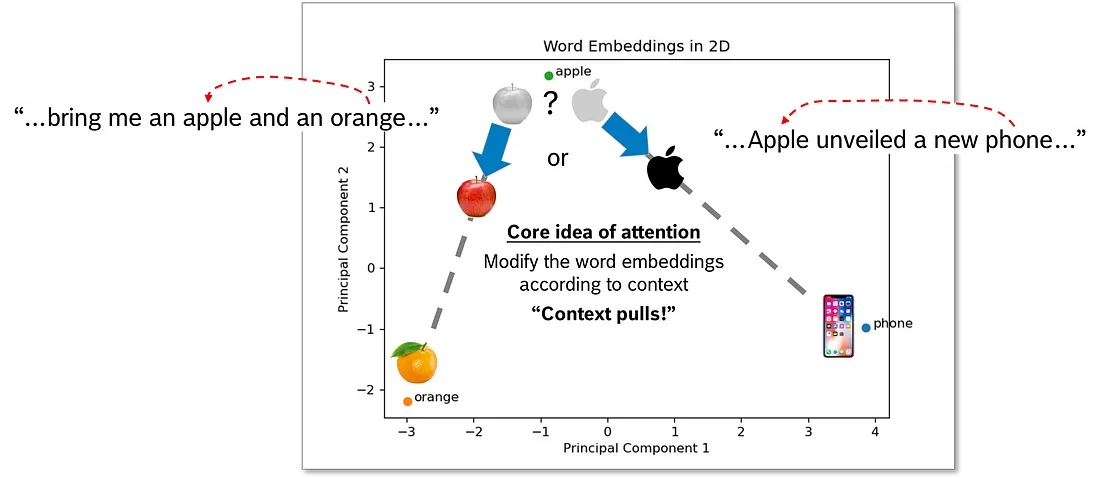
在我们谈论水果的情况下, 我们会将"apple"的词嵌入移近"orange”, 而在谈论科技公司的情况下, 我们会将其移到"phone"的位置。
如何教计算机理解"apple"是与"phone"还是"orange"有关?我们需要计算 “apple” 和上下文中所有其他单词之间的单词亲和力 — 包括它本身。这告诉我们哪里有强亲和力, 哪里有弱亲和力。事实上, 我们计算了上下文中所有词元组合之间的词语亲和力。最后, 根据亲和力, 我们修改单词嵌入, 并将具有更强上下文的标记移得更近。
计算相似度的方法有多种, 通常称为相似度。在这里, 我们使用了缩放的点积, 这也是在论文 “Attention Is All You Need” 中提出的。缩放的点积是我们评估的两个词元的词嵌入向量 a 和 b 之间的点积除以词嵌入向量的维度数 d 的平方根。

图显示了 “bring me an apple and an orange” 上下文中所有标记组合的缩放点积亲和力。正如我们在表格的最后一列中看到的, 行的总和大约在 10 到 18 之间。对于新单词嵌入的计算, 正好为 1 的总和更方便。为了实现这一点, 我们使用 softmax 函数:
根据方程, softmaxing 意味着将一行的每个值都取到 e, 并将其除以所有值之和到 e。在我们的示例中, 在应用 softmax 后, 我们得到了所示的值。
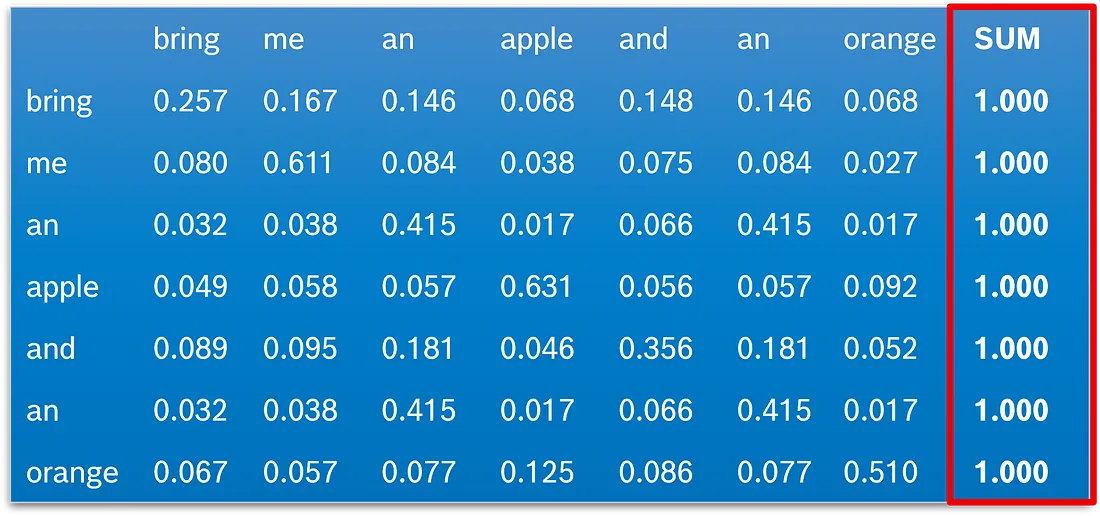
图中的亲和力是计算上下文调整的"动态"词嵌入向量的系数: 亲和力越高, 标记对新嵌入的影响就越大。让我们以 “apple” 为例(图中的第四行):
“apple” 的上下文调整的 “dynamic” 嵌入是上下文中所有标记的乘积之和乘以 “apple” 与该特定标记的亲和力。在我们的示例中, “apple” 的单词 embedding 仅保持原来的 63.1%, 并且修改了 36.9% 以更好地适应其上下文。方程中的 “bring” 等指的是嵌入向量。在向量表示法中, 方程如下所示:
1.5.2 查询、键和值矩阵
查看论文 “Attention Is All You Need”, 我们会发现一种修改后的方法, 其中包含所谓的查询 Q、键 K 和值 V 矩阵。
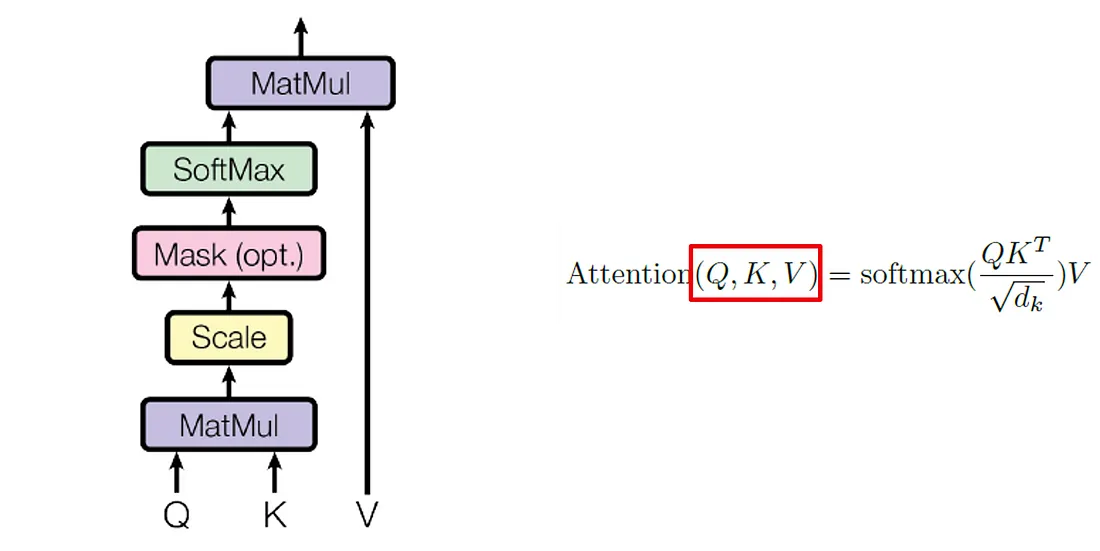
通过查询 Q、键 K 和值 V 矩阵, 我们在注意力机制中添加了额外的反向传播学习。矩阵可帮助模型在给定上下文中找到更好的单词嵌入。现在, 让我们专注于查询 Q 和键 K 矩阵。值 V 稍后出现。
如果我们从数学中回想一下, 将向量与矩阵几何相乘意味着变换。此转换会拉伸、压缩、旋转或扭曲向量空间。
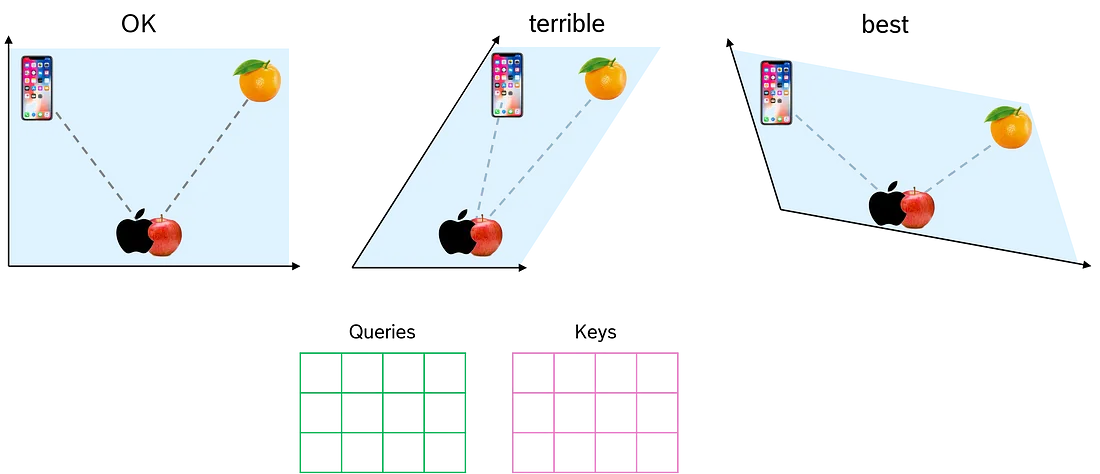
为什么我们会扭曲向量空间?这个想法是找到一个非常适合在特定上下文中表示标记含义的空间。
在图中, 我们看到左侧平面可以分隔单词 “apple” 的两个含义。中间平面做得很糟糕, 因为即使我们将单词 “apple” 移近 “phone” 或 “orange”, 我们仍然将这两个表示非常接近。第三个平面显然是最好的。它强烈支持将 “apple” 的两个含义分开。
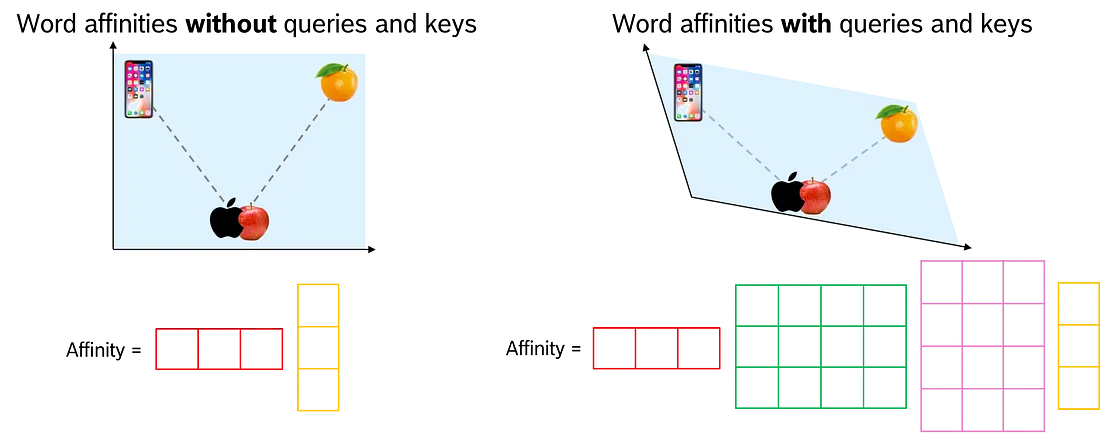
通过查询 Q 和键 K 矩阵, 我们让 transformer 网络找到捕获标记上下文的最佳参数。因此, 我们将这两个矩阵添加到单词亲和力的计算中。我们不是直接将两个嵌入向量相乘, 而是将第一个嵌入向量和 Q 矩阵(本身就是一个向量)的乘积与第二个嵌入向量和 K 矩阵的(转置)乘积相乘。
在没有查询 Q 和键 K 矩阵的情况下, 我们使用给定的向量空间。通过 Q 和 K, 我们找到了一个最佳向量空间, 从而根据输入句子的上下文找到更好的动态词嵌入。
有和没有 Q 和 K 矩阵的缩放点积比较
在查询 Q 和键 K 矩阵中找到的向量空间针对单词亲和力进行了优化。值矩阵 V 准备下一步, 即计算给定上下文之后下一个标记的概率。因此, 我们计算了第三个线性变换, 它为我们提供了一个针对此任务优化的向量空间。
已经考虑了一个只有一个 token 作为 input 的玩具示例。关于第 2 部分中的代码示例, 我想演示如果我们输入整个句子, 矩阵运算是什么样子的。从那里, 很容易得出现实生活中的矩阵运算的结论。

在图中, 红色的 7x3 矩阵 X 表示输入句子及其嵌入向量。每行对应一个标记。这三列是单词 embedding 的三个维度。请记住, 现实生活中的单词嵌入有成百上千个维度!
绿色的 3x4 矩阵是我们的查询矩阵 Q, 它为注意力模型增加了额外的学习能力。这三行是固定的, 因为它们需要对应于 X 的嵌入维度。这四列称为 “head-size”, 是 transformer 模型的超参数。理论上, 我们可以选择任何值。列数越多, 学习能力越强。
键矩阵 K 的大小始终与查询矩阵 Q 的大小相同。因此, 它的维度为 3x4, 但在图中, 它被转置为 4x3。黄色输入矩阵 X 也是如此, 它对应于红色输入矩阵。
乘法运算返回一个 7x7 矩阵, 其中包含输入句子中每个可能的标记组合的未缩放的亲和力。
到目前为止, 我们省略了缩放和 softmaxing, 但这两个步骤都非常简单, 并且与我们在第 1.5.1 章中讨论的内容几乎相同。
在计算查询矩阵 Q 和键矩阵 K 的点积后立即应用缩放。我们只需将未缩放的亲和力的 7x7 矩阵的每个值除以嵌入维度 \(\sqrt{d}\) 的平方根。
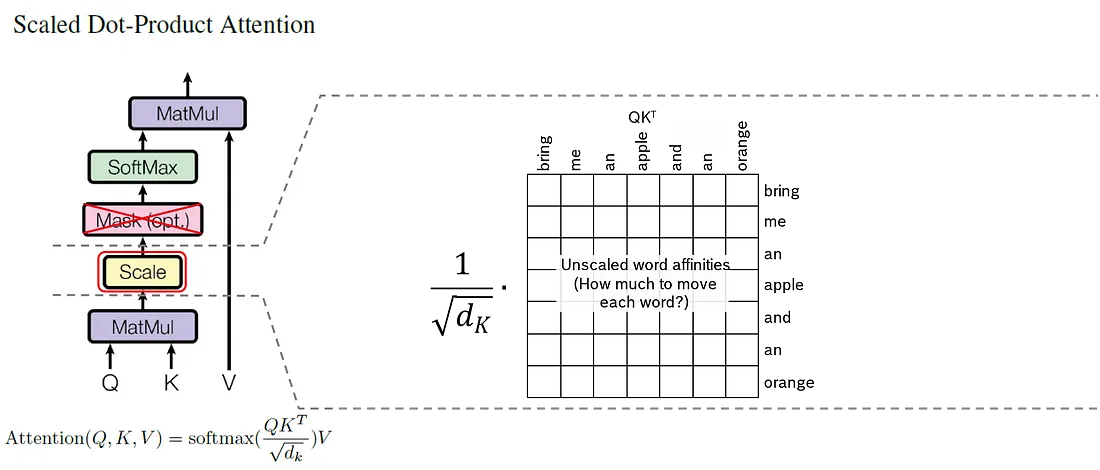
缩放后的下一步是 softmaxing。与缩放一样, softmax 是按元素应用的, 每个元素除以相应行的总和。
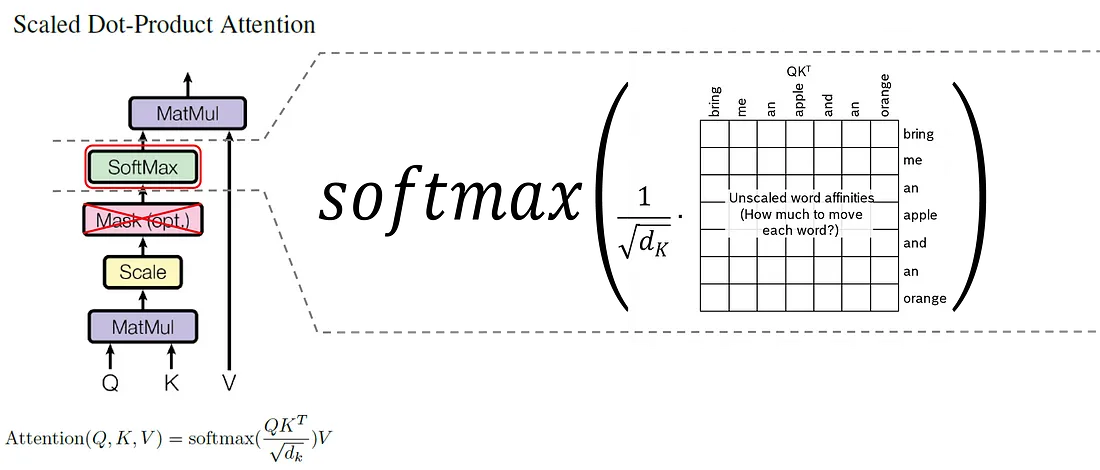
最后, 总结一下注意力矩阵作的步骤:
- 我们计算 X * Q * K_transposed * X_transposed 的矩阵乘积, 并接收未缩放的亲和力作为 7 个输入标记的 7x7 矩阵。
- 我们将 7x7 矩阵的每个元素除以 \(\sqrt{d}\) 。这为我们提供了缩放的亲和力。缩放对于 softmax作很重要, 因为初始值应该很小。
- 掩码是原始论文中提到的可选步骤, 但在 ChatGPT 中未应用。我们忽略它。
- 我们对缩放的亲和力矩阵进行 softmax 。因此, 7x7 矩阵的每一行加起来都是 1。
- 最后, 我们将缩放和软最大化的单词亲和力 7x7 矩阵与 X * V 相乘, 并接收上下文调整的单词嵌入作为最终结果。
1.5.3 多头注意力
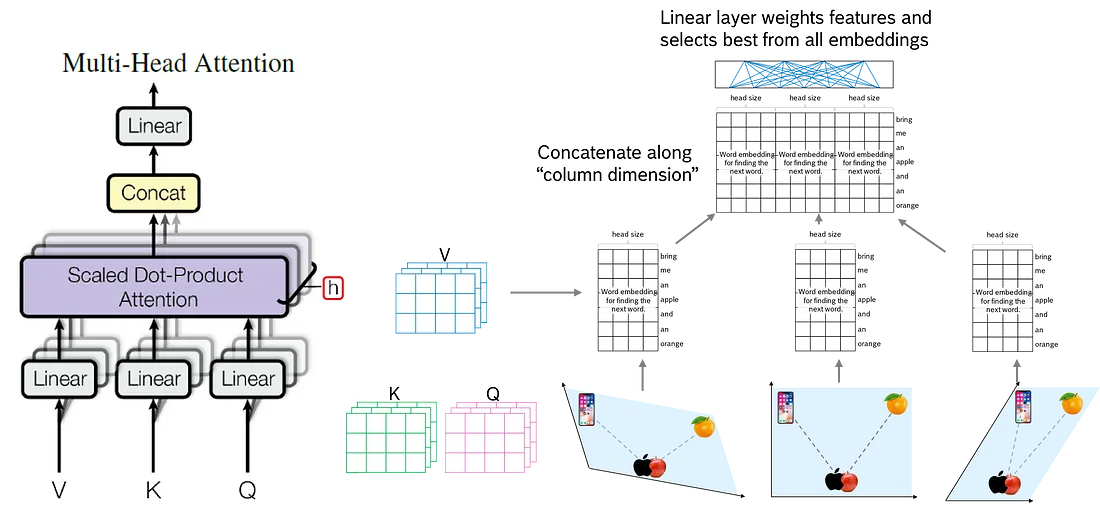
但是 ChatGPT 和其他变形金刚有 h-many 这样的 h-many。这意味着我们并行计算 h 个查询、键和值矩阵。这让我们 h 尝试找到一个好的嵌入, 从而得到 h 7x4 的结果矩阵。
如何处理 h 结果矩阵?我们沿列轴将它们连接起来, 并在连接矩阵的顶部定义一个完全连接的中性网络(“线性层”), 每列一个节点。线性层的任务是对串联结果矩阵中的信息进行加权: 有用的信息获得较高的权重, 而不太有用的信息获得较少的权重。这样, 变压器就学会了采摘樱桃。
1.6 层范数
注意力机制为我们提供了 “动态” 嵌入向量 — 包括标记位置和标记之间的关系。在接下来的步骤中, 我们打算计算字典中所有标记的概率值, 作为 LLM 的下一个输出。在我们这样做之前, 我们需要一个更具技术性的步骤: Layer Norm
Layer Norm 是深度学习模型中常用的一种技术, 可以提高模型在训练过程中的稳定性和收敛性。它将指定维度(在本例中为嵌入向量)上的值标准化为平均值 = 0 且标准差≈ 1。
假设我们有两个嵌入深度为 5 的嵌入向量。这给了我们一个大小为 (2, 5) 的张量。出于演示目的, 我们使用 0 到 10 之间的随机数实例化张量。
import torch
import torch.nn as nn
# Define word embedding vectors
x = torch.rand(2, 5)*10
print("Original input tensor:")
print(x)
接下来, 我们实例化一个 Layer Norm 并将输入形状定义为每个嵌入向量的 5 个值。我们通过 Layer Norm作运行张量, 输出转换后的张量并检查新的平均值和新的标准差。
# Apply layer normalization
layer_norm = nn.LayerNorm(x.size()[1])
normalized_x = layer_norm(x)
print("Normalized input tensor:")
print(normalized_x)
print("\nMean:")
print(normalized_x.mean(dim=1))
print("\nStandard deviation:")
print(normalized_x.std(dim=1, unbiased=False))
我们看到, 值范围从大约 -1.6 到 +1.6, 平均值接近 0, 标准差为 1。
1.7 前馈
前馈层是 transformer 中的计算引擎。它接收我们输入的规范化和上下文调整(“动态”)词嵌入, 并承担计算下一个标记的概率值的任务。它具有与嵌入向量具有维度一样多的输入节点, 并且在 LLM 的词汇表中, 每个标记都有一个输出节点。该层是完全连接的, 因此每个嵌入维度都与词汇表中的每个标记都有关系。
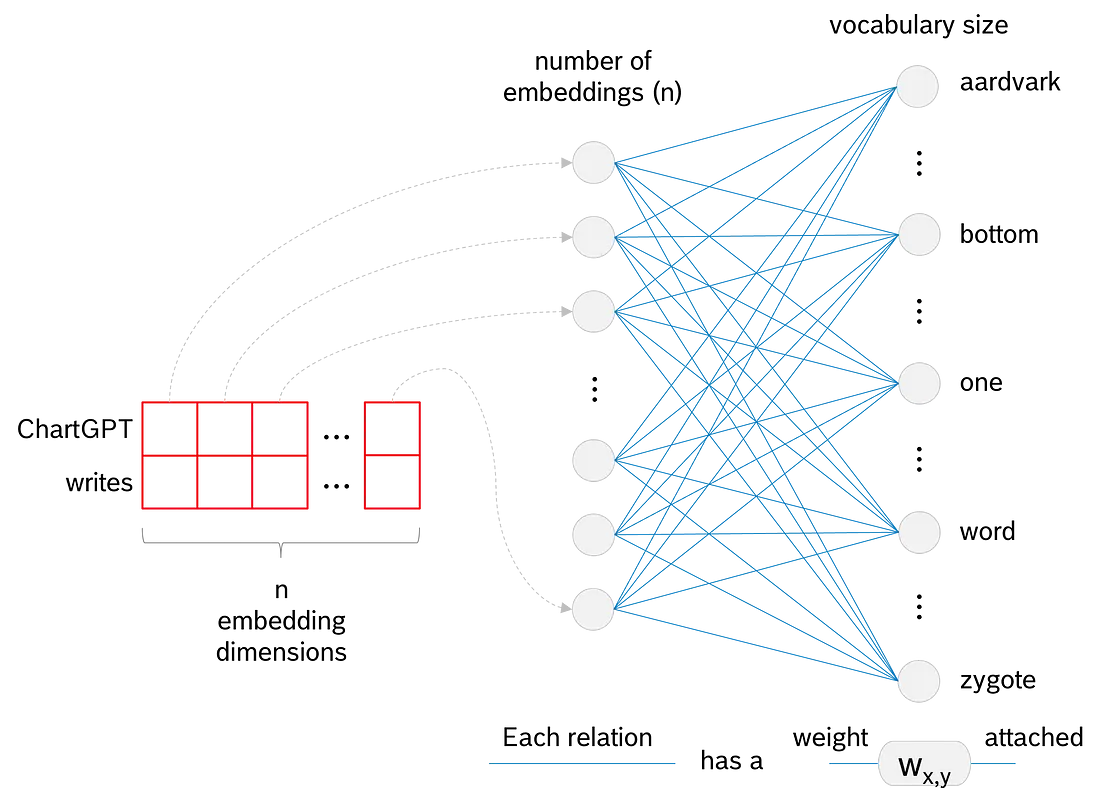
图延续了我们 “ChatGPT writes…” 的例子。我们看到两个输入标记 “ChatGPT” 和 “writes”。这两个 token 都有大小为 n 的嵌入向量, 这些向量将其值输入到前馈网络的 n 个输入节点中。模型训练期间的任务是学习最佳权重, 将嵌入值转换为下一个标记的概率值, 以遵循"ChatGPT writes…"。
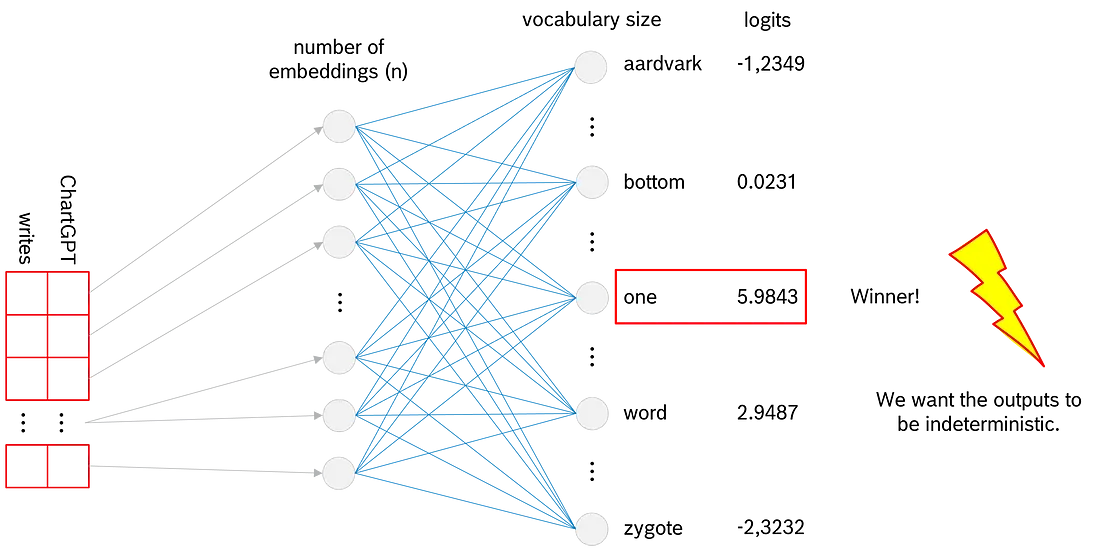
在神经网络中, 使用一组给定的权重, 我们可以计算 logits 作为前馈层的输出。价值最高的 Token 是搜索下一个 Token 的潜在获胜者。所以, 从理论上讲, 我们可以在这一点上停下来!但事实上, 这不是 ChatGPT 的工作原理。如果我们到此为止, ChatGPT 会对相同的提示给出完全相同的答案。但是, 正如我们所知, 如果我们输入相同的提示, ChatGPT 提供的答案略有不同。因此, 我们的模型需要一些随机性。为了给模型提供这个特性, transformer 架构还有两个步骤: softmax 和 multinomial。
1.8 Softmax
我们想给 LLM 一个不确定的行为。实现此目的的第一步是将上一步(前馈)的 logits 转换为 0 到 1 之间的概率。使用 softmax, 我们将每个值都取到 e 并将其除以所有值之和到 e。
softmaxing 有什么效果?
- 将每个值都取到 e 有助于我们对负 logit 值进行作。接近 0 的负值将转换为接近 1 的值, 而接近负无穷大的负值将转换为 0。
- 将每个值除以所有值的总和可保证所有概率的总和为 1。
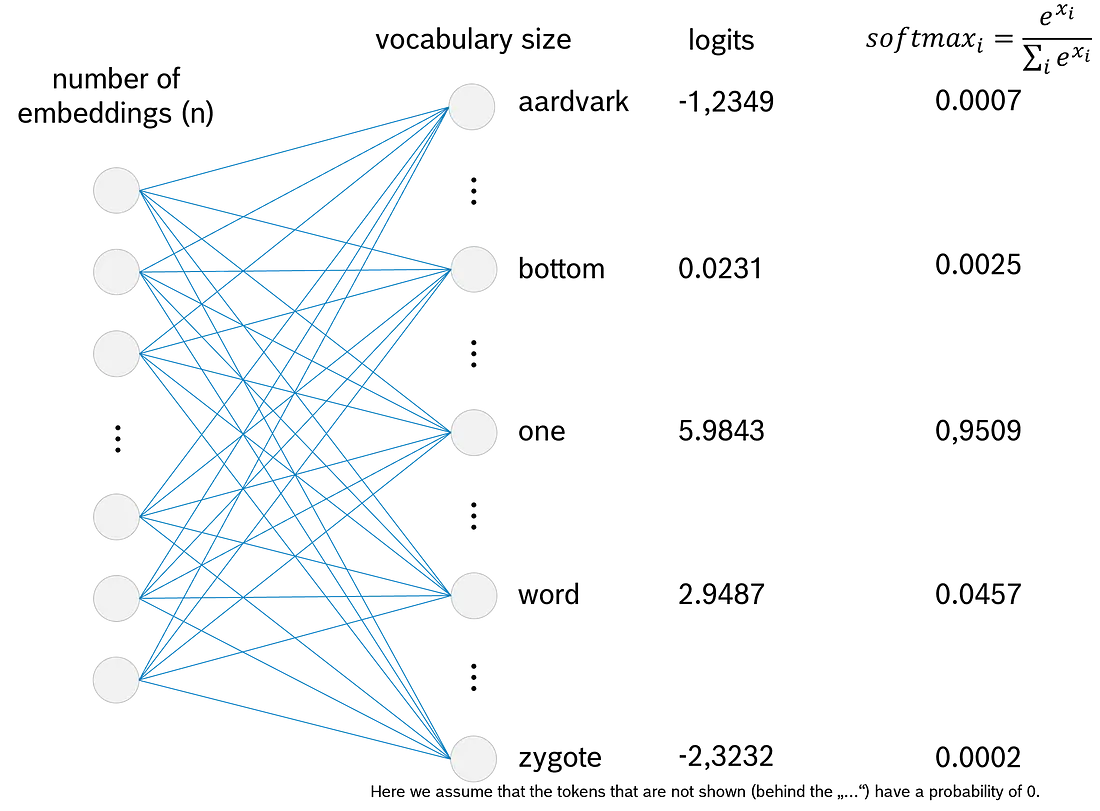
总之, softmax 将 logit 转换为值介于 0 和 1 之间的适当概率, 确保所有概率之和等于 1。
1.9 多项式
我们已经计算了 LLM 词汇表中每个标记的概率。现在, 是时候从多项式分布函数中抽取样本了。
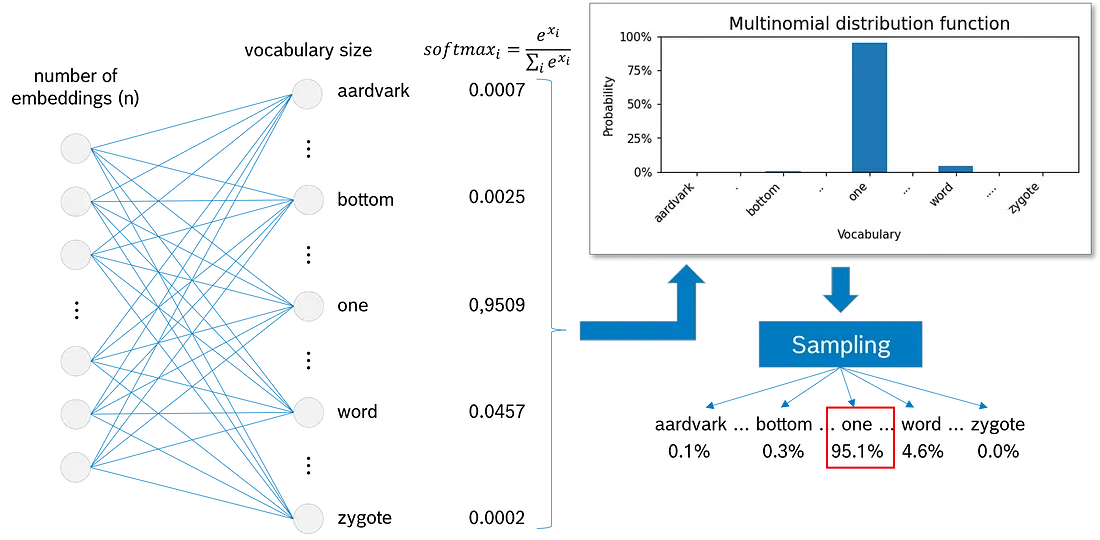
图说明了采样过程:
- “aardvark”(英语词典中的第一个单词)将被选择, 可能性为 0.1%。
- bottom 0.3%。
- 最有可能的是, “one"将被抽样, 因为它的可能性为 95.1%。
- “word” 的概率为 4.6%。
- 而 “zygote”(英语词典中的最后一个单词)几乎是不可能的, 四舍五入的可能性为 0.0%
我们讨论的所有内容都是通过 transformer 的一个循环, 我们已经决定了接下来要输出的一个 token。我们一次又一次地对串联的输入重复相同的过程, 直到
令牌被采样为下一个输出!
2. 在代码中实现
将编写一个Fairy_Tale_GPT, 该 从一系列童话故事(格林兄弟和 H.C. 安徒生兄弟)中学习英语单词。这些数据可从 Gutenberg Project 免费获得。事实上, 数据的内容不如免费使用文本本身的可用性重要。您也可以使用其他数据。
为了保持模型相对较小, 我们将使用童话文本中的字符作为我们的标记, 而不是单词或单词片段。这使得模型的词汇量较小。我也尝试用词元来训练模型(这在原则上是可行的), 但对训练数据的需求明显高于我们现有的数据。因此, 学习成功非常有限。
该Fairy_Tale_GPT基于 Andrej Karpathy 名为 nanoGPT 的项目。如果您想查看 Andrej 的原始模型和解释, 请查看他的 YouTube 视频。
2.1 数据准备
import torch
import torch.nn as nn
from torch.nn import functional as F
import matplotlib.pyplot as plt
from IPython.display import clear_output
torch.manual_seed(1337)
# We load the text file's content into the variable 'text'.
with open('Fairy_Tales.txt', 'r', encoding='utf-8') as f:
text = f.read()
2.2 分词化
分词化是将数据拆分为单词、单词片段或字符, 找到唯一标记并为它们分配唯一编号的过程。分词化背后的想法是限制 LLM 词汇表的大小, 并准备模型来处理这些分词。
# Find a list of all unique characters in the text.
# The data type 'set' eliminates all doubles.
chars = sorted(list(set(text)))
vocab_size = len(chars)
print(''.join(chars))
print('\nSize of vacabulary: ', vocab_size)
接下来, 我们需要一个编码和解码函数来将标记(在本例中为字符, 在其他应用程序中为单词或单词片段)转换为标记编号。第一步, 我们定义两个字典: 一个用于 token → number, 另一个用于 number → token。
# Dictionary: Characters (c) to numbers (i)
ctoi = {c:i for i,c in enumerate(chars)}
# Dictionary: Numbers (i) to characters (c)
itoc = {i:c for i,c in enumerate(chars)}
稍后, 我们将数据拆分为训练数据集和验证数据集。例如, 接受前 90% 作为训练数据, 接受其余 10% 作为验证数据, 这意味着使用与用于训练不同的童话故事进行验证。这听起来并不理想。因此, 我们将完整的数据集拆分为多个段落。这允许我们在将数据划分为训练数据集和验证数据集时混合段落。
# Split the full text into paragraphs of min 50 words
# Return a list of lists
def split_text_into_paragraphs(text, min_words=50):
lines = text.split('\n')
current_paragraph = ""
paragraphs = []
for line in lines:
# Add line to the current paragraph buffer
current_paragraph += line + "\n"
# If current paragraph has at least 'min_words' words, store it and reset
if len(current_paragraph.split()) >= min_words:
paragraphs.append([current_paragraph])
current_paragraph = ""
# Add left-overs
if current_paragraph:
paragraphs.append([current_paragraph])
return paragraphs
现在我们可以继续编码和解码了。该函数接受以字符串作为变量和字典的列表列表(阅读 “ctoi”)。它列举了 、获取文本, 并根据字典对它们进行编码。最后, 将编码附加到列表并输出。
# Encode strings to list of integers
def encode(paragraphs, ctoi):
"""
Translates a list of lists with text into a
list of lists with token numbers.
"""
encoded_paragraphs = []
for paragraph in paragraphs:
# Get text from inner list
text = paragraph[0]
# Translate tokens to integers
encoded = [ctoi[c] for c in text if c in ctoi]
# Add the encoded paragraph to the list
encoded_paragraphs.append(encoded)
return encoded_paragraphs
# Decode list of numbers (li) to string (s)
def decode(li, itoc):
"Translates a list of integers back to a sting."
# Translate integers to tokens
tokens = [itoc[i] for i in li]
# Join tokens to a string
decoded_text = "".join(tokens)
return decoded_text
下一步是对整个数据集进行编码。这会将字符串列表转换为整数列表列表。
# Encode the full dataset
data = encode(split_text_into_paragraphs(text), ctoi)
现在, 我们将段落(整数标记数字)随机排列并将它们拆分为 training dataset 和 validation dataset 。
import random
# Shuffle data
random.shuffle(data)
# Split data into train (90%) and val (10%)
n = int(0.9*len(data))
train_data_list = data[:n]
val_data_list = data[n:]
到目前为止, 这两个数据集都是 Python 整数列表。但对于 LLM, 我们需要 PyTorch 张量。由于我们不打算进一步修改验证数据集, 因此我们可以立即将其转换为 PyTorch 张量。为此, 我们将整数列表展平为单个整数列表, 并将数据加载到 PyTorch 张量中。
# Flatten the list of lists into a single list
flat_list = [token for paragraph in val_data_list for token in paragraph]
# Load validation data into PyTorch tensor
val_data = torch.tensor(flat_list, dtype=torch.long)
2.3 数据馈送器功能
数据馈送器为模型提供训练数据和相应的标签, 或者在验证的情况下, 为模型提供验证数据。
首先, 我们定义了三个重要的模型参数。
- batch_size确定在一个训练循环期间并行处理多少个数据块。我们将其设置为 64。
- block_size定义模型在计算下一个 Token 时看到的上下文长度。我们将其设置为 128 个令牌。
- device是 ‘cuda’ 或 ‘cpu’, 并确定模型是在计算机的 CPU 还是 GPU 上处理。
batch_size = 64 # Number of independent sequences we process in parallel
block_size = 128 # Length of token sequences as context
device = 'cuda' if torch.cuda.is_available() else 'cpu' # Use GPU instead of CPU, if available
print(device)
# Function, that provides the model with a batch of training or validation data
# and the corresponding labels (the correct next token)
def get_batch(ValTrain):
# Define data source
if ValTrain == "val":
data = val_data
else:
# Flatten and shuffle the training data (data augmentation)
shuffled_data = [
token for paragraph in random.sample(train_data_list, len(train_data_list))
for token in paragraph
]
data = torch.tensor(shuffled_data, dtype=torch.long)
# Generate sliding windows over the data
sliding_windows = [
data[i:i + block_size + 1]
for i in range(0, len(data) - block_size, block_size // 2) # Step size = block_size // 2
]
# Select batch_size many windows randomly
selected_windows = random.sample(sliding_windows, batch_size)
# Split each window into input (x) and target (y)
x = torch.stack([window[:-1] for window in selected_windows]) # All but the last token
y = torch.stack([window[1:] for window in selected_windows]) # All but the first token
# Move tensors to device (CPU/GPU)
x, y = x.to(device), y.to(device)
return x, y
当我们测试get_batch()该函数时, 我们看到 input_data和 labels是大小为 (64, 128) 的张量, 并且labels向右移动了一个标记。
# Test the feeder function
input_data, labels = get_batch('train')
print("Shape of input_data:", input_data.shape, "\n")
print("Input_data:\n", input_data, "\n")
print("labels:\n", labels, "\n")
2.4 注意头
注意力头是多头注意力的一部分, 而多头注意力本身就是注意力块的一部分。图显示了多头注意力中注意力头的位置。在接下来的步骤中, 我们将经常引用该图, 因此请牢记这一点。
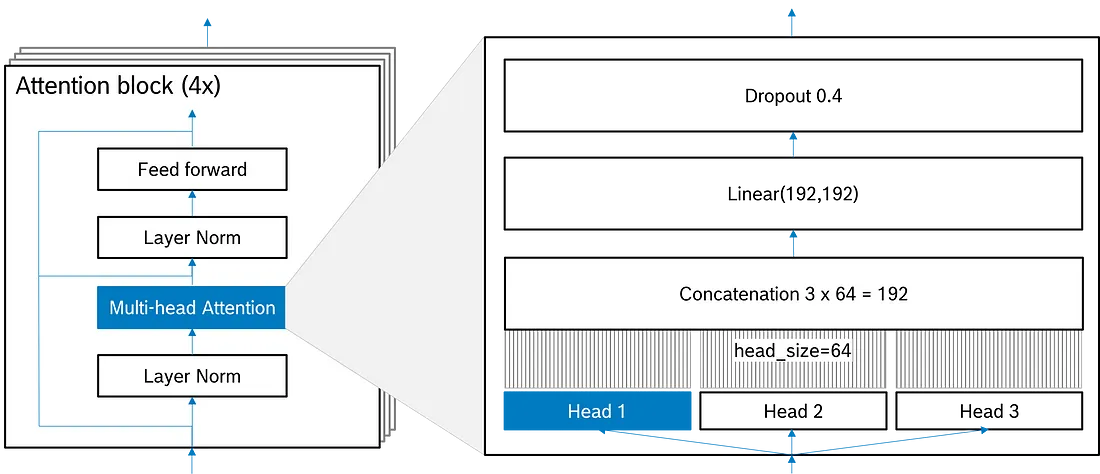
我们从两个额外的超参数开始编码:
- n_embd定义所有标记的嵌入深度。我们将其设置为 192。
- dropout是我们在训练期间随机设置为 0 的参数的百分比。这是防止过度拟合的措施。由于模型倾向于记住数据而不是泛化模式(可能是由于数据集的大小不足), 我们设置dropout为相对较高的值 0.4。
# More hyperparameters
n_embd = 192 # The embedding depth for each token
dropout = 0.4 # The percentage of weights we set to 0 during training for regularization
# Class for single attention head
class Head(nn.Module):
""" Single head of self-attention """
def __init__(self, head_size):
super().__init__()
self.key = nn.Linear(n_embd, head_size, bias=False) # (C,H)
self.query = nn.Linear(n_embd, head_size, bias=False) # (C,H)
self.value = nn.Linear(n_embd, head_size, bias=False) # (C,H)
self.register_buffer('tril', torch.tril(torch.ones(block_size, block_size))) # Lower triangular matrix
self.dropout = nn.Dropout(dropout) # Ignore a portion of neurons per training loop --> prevent overfitting
def forward(self, x):
B,T,C = x.shape # C=n_embd
k = self.key(x) # x @ key (B,T,C) @ (C,H) --> (B,T,H)
q = self.query(x) # x @ query (B,T,C) @ (C,H) --> (B,T,H)
# compute attention scores ("affinities")
wei = q @ k.transpose(-2,-1) * C**-0.5 # (B,T,H) @ (B,H,T) -> (B,T,T)
wei = wei.masked_fill(self.tril[:T, :T] == 0, float('-inf')) # (B,T,T) # Fill with '-inf' where template has 0
wei = F.softmax(wei, dim=-1) # (B,T,T)
wei = self.dropout(wei) # (B,T,T)
# Perform the weighted aggregation of the values
v = self.value(x) # x @ value (B,T,C) @ (C,H) --> (B,T,H)
out = wei @ v # (B,T,T) @ (B,T,H) --> (B,T,H)
return out
2.5 多头注意力
多头注意力并行利用n_head注意力头。此外, 我们应用了一个线性层来加权, 越有益的注意力头部反应越高, 越不有益越低。
# Class that bundles 3 attention heads
class MultiHeadAttention(nn.Module):
""" Three heads of self-attention in parallel """
def __init__(self, num_heads, head_size):
super().__init__()
self.heads = nn.ModuleList([Head(head_size) for _ in range(num_heads)]) # Just a container
self.weighting = nn.Linear(n_embd, n_embd) # Linear layer to weight the attention heads
self.dropout = nn.Dropout(dropout) # Prevent overfitting
def forward(self, x):
out = torch.cat([h(x) for h in self.heads], dim=-1) # Feed parallel attention heads and concatenate results
out = self.dropout(self.weighting(out)) # Weighting the attention head results and dropout
return out
2.6 注意力块的前馈
注意力块中的前馈层具有通用的计算目的, 由四个步骤组成。因此, 我们将其定义为自己的类 。
# A linear layer for general calculation purpose
class FeedForward(nn.Module):
""" Simple linear layer followed by a non-linearity """
def __init__(self, n_embd):
super().__init__()
self.net = nn.Sequential( # Sequence of steps
nn.Linear(n_embd, 4 * n_embd),
nn.ReLU(),
nn.Linear(4 * n_embd, n_embd),
nn.Dropout(dropout))
def forward(self, x):
return self.net(x)
2.7 注意块
同样, 我们定义了一个名为Block()的新类。在其__init__()方法中, 我们计算 Q、K 和 V 矩阵的自由维数 — head_size — 作为嵌入深度 n_embd 和注意力头数 n_head 的商。然后, 我们实例化self.sa 中的类 MultiHeadAttention() 和 self.ffwd 中的 FeedForward()类。此外, 我们在变量 self.ln1 和 self.ln2 中定义了两个归一化层。
# Only one pass-through. Loop is specified in the Transformer class
class Block(nn.Module):
""" Attention block """
def __init__(self, n_embd, n_head):
super().__init__()
head_size = n_embd // n_head # Free dimension of key, query and value matrices
self.sa = MultiHeadAttention(n_head, head_size)
self.ffwd = FeedForward(n_embd)
self.ln1 = nn.LayerNorm(n_embd)
self.ln2 = nn.LayerNorm(n_embd)
def forward(self, x):
x = x + self.sa(self.ln1(x)) # Residual/skip connection
x = x + self.ffwd(self.ln2(x)) # Residual/skip connection
return x
2.8 变压器类
在生产过程中, 我们没有任何标签。相反, 我们感兴趣的是模型的输出作为对用户交互的响应。我们向模型提供输入数据并将其传递给模型 - 与训练相比, 这一次增加了两个步骤。在 Feed forward 层之后, logit 被 softmax 并在 Multinomial distribution 函数中用于对下一个标记进行采样。
根据Transformer()训练和生产过程中的不同方法, 该类有三种方法: init_(), forward()和 generate()
# More hyperparameters
n_head = 3 # Number of attention heads in multi-head attention
n_layer = 4 # Number of attention blocks
# Main class embracing all modules
class Transformer(nn.Module):
# When we instantiate from the Transformer class
def __init__(self):
super().__init__()
self.token_embedding_table = nn.Embedding(vocab_size, n_embd) # Word/token embedding
self.position_embedding_table = nn.Embedding(block_size, n_embd) # Positional embedding
self.blocks = nn.Sequential(*[Block(n_embd, n_head) for _ in range(n_layer)]) # Stack of attention blocks
self.final_ln = nn.LayerNorm(n_embd) # Final layer norm
self.final_ff = nn.Linear(n_embd, vocab_size) # Final linear layer
# When we pass data through an instance of the Transformer class
def forward(self, input, targets=None): # input and targets are both (B,T)-dimensional tensors of integers
B, T = input.shape # Dimensions of input data: batch x tokens
tok_emb = self.token_embedding_table(input) # (B,T,C)
pos_emb = self.position_embedding_table(torch.arange(T, device=device)) # (T,C)
x = tok_emb + pos_emb # (B,T,C), Python automatically adds dimension B to pos_emb
x = self.blocks(x) # (B,T,C)
x = self.final_ln(x) # (B,T,C)
logits = self.final_ff(x) # (B,T,vocab_size)
# Only if targets are defined --> loss calculation
if targets is None:
loss = None
else:
B, T, C = logits.shape # Get dimensions of output
logits = logits.view(B*T, C) # Transform to two dimensions for cross_entropy function
targets = targets.view(B*T) # Transform to one dimension for cross_entropy function
loss = F.cross_entropy(logits, targets) # Calculate the losses
return logits, loss
# When we generate new text (production)
def generate(self, idx, max_new_tokens):
# idx is (B, T) tensor of indices
for _ in range(max_new_tokens): # Concatenate max_new_tokens outputs
# Crop idx to the last block_size tokens
idx_cond = idx[:, -block_size:]
# Get the predictions
logits, loss = self.forward(idx_cond)
# Focus only on the last token
logits = logits[:, -1, :] # becomes (B, C)
# Apply softmax to get probabilities
probs = F.softmax(logits, dim=-1) # (B, C)
# Sample from the distribution
idx_next = torch.multinomial(probs, num_samples=1) # (B, 1)
# Append sampled index to the running sequence
idx = torch.cat((idx, idx_next), dim=1) # (B, T+1)
return idx
2.9 实例化 Transformer
我们已经定义了 Fairy_Tale_GPT 的所有类。因此, 我们可以在开始模型训练之前实例化它并对其进行第一次尝试。
# Instantiate an object from the Transformer class
model = Transformer().to(device) # 'model' lives on the device, in my case the GPU
# Print the number of parameters of the model
print(format(sum(p.numel() for p in model.parameters()),","), 'parameters')
# Generate from the model
context = torch.zeros((1, 1), dtype=torch.long, device=device)
untrained_results = decode(model.generate(context, max_new_tokens=200)[0].tolist(),itoc)
print(untrained_results)
2.10 模型训练
# Cosine annealing learning rate scheduler
from torch.optim.lr_scheduler import CosineAnnealingLR
# More hyperparameters
eval_iters = 10 # How many iterations do we average in the loss calculation
learning_rate = 1e-3 # Starting step size for learning
max_iters = 10000 # Number of training loops
eval_interval = 200 # How often evaluate the model performance
context_tensor = torch.zeros((1, 1), dtype=torch.long, device=device)
# Function calculates losses and averages results over eval_interval values
@torch.no_grad() # Do not calculate any gradients for this function
def estimate_loss():
out = {} # Empty dictionary for the results
model.eval() # Set model to evaluation mode
# Calculate loss for training and validaton data
for split in ['train', 'val']:
losses = torch.zeros(eval_iters) # Set to 0 for start
for k in range(eval_iters): # 10 loops
X, Y = get_batch(split) # Get training data
logits, loss = model(X, Y) # Call model and get logits and losses
losses[k] = loss.item()
out[split] = losses.mean() # Save average under key 'train' or 'val'
model.train() # Set model in training mode
return out
对于模型训练, 我们定义了 learning_rate。它根据反向传播的梯度和学习率更新模型参数。我们选择非常常见的优化器。优化器允许指定将所有权重之和(乘以指定因子 0.03)添加到损失函数中。这促使模型更喜欢较小的权重 — 这也是防止过度拟合的措施。
# Create a PyTorch optimizer
optimizer = torch.optim.AdamW(model.parameters(), lr=learning_rate, weight_decay=0.03)
# Cosine annealing learning rate scheduler
scheduler = CosineAnnealingLR(optimizer, T_max=max_iters, eta_min=1e-5) # Minimal LR is 1e-5
# Empty lists of losses
loss_lst_train = []
loss_lst_val = []
loss_lst_x = []
# Train the model over max_iter loops
for iter in range(max_iters):
# Get a batch of training data
xb, yb = get_batch('train')
# Run the transformer model
logits, loss = model(xb, yb)
# Zero the gradients
optimizer.zero_grad(set_to_none=True)
# Calculate the gradients
loss.backward()
# Optimize parameters through backpropagation
optimizer.step()
# Update the learning rate with the scheduler
scheduler.step()
# Evaluate and print losses
if iter % eval_interval == 0 or iter == max_iters - 1:
# Caluculate losses
losses = estimate_loss() # Call evaluation function
loss_lst_train.append(losses['train'].item()) # Append to training list
loss_lst_val.append(losses['val'].item()) # Append to validaton list
loss_lst_x = list(range(len(loss_lst_train))) # Prepare the x values for plotting
# Plot
clear_output(wait=True) # Clear output in jupyter
print(f"Step {iter}: train loss {losses['train']:.4f}, val loss {losses['val']:.4f}")
plt.figure(figsize=(5,3))
plt.plot(loss_lst_x,loss_lst_train,label='train')
plt.plot(loss_lst_x,loss_lst_val,label='val')
plt.xlabel('steps (x' + str(eval_interval) + ')')
plt.ylabel('losses')
plt.title('Training and validation loss')
plt.legend()
plt.show()
# Do a test generation to observe the quality
print('Test word generation:')
print(decode(model.generate(context_tensor, max_new_tokens=200)[0].tolist(),itoc))
模型训练后, 我们应该保存参数。否则, 从 PC 内存中删除模型后, 它们将丢失, 我们将不得不重新启动训练。
torch.save(model.state_dict(), 'Name_of_your_choice.pth')
2.11 生成新 Token
在我们开始生成 token 之前, 让我们加载模型参数。在这里, 我们假设它本身已经加载。
# Load the saved model state
state_dict = torch.load('Name_of_your_choice.pth')
# Load the parameters into the transformer model
model.load_state_dict(state_dict)
现在, 让我们比较一下训练前后 LLM 的输出。
# Print output before training
print('Model output before training:')
print(untrained_results)
# Print output after training
context = torch.zeros((1, 1), dtype=torch.long, device=device)
trained_results = decode(model.generate(context, max_new_tokens=500)[0].tolist(),itoc)
print('\nModel output after training:')
print(trained_results)
参考
From Concept to Code: Unveiling the ChatGPT Algorithm
Attention Mechanisms in LLMs

