Iawen's Blog

风无形，水无势，互联网没有昼夜。趁这些许的闲暇时光，随手采摘或记录着这知识海洋的点点滴滴......

笔记导航

最新笔记

首页 > 数据科学 深度学习中常见的数据处理方法 2025-10-29 18:55:46

目录

近几年, 随着硬件算力设备和算法模型逐渐在标准化、模块化发展的趋势下, 数据成为了最不可控的变量。从算力、算法、数据三大基本要素来看, 算力是最容易作为标准化来衡量的, 而且通用性最高, 可以在任何深度学习任务中都能够使用, 比如使用Tesla V100可以做一般的检测分类任务、分割任务、生成任务, 也可以做普通的语言模型任务、强化学习模型任务等。

数据作为三者之中不容易用标准化的元素来说, 其不可控的原因主要是由于不同的任务要使用不同的数据集, 所以很难对数据做到真正的标准化和模块化, 无法像算法模型一样直接对其调用。在学术界, 真正通用的数据就那么几个, 比如COCO数据集, VOC数据集, ImageNet数据集, 都是用来发表论文时使用的, 在工业界, 大多数任务都是指定的数据, 无法直接使用这类数据集的, 最多也就是使用其数据作为预训练的模型。比如很多知名的神经网络模型, 像早期的ResNet, 后来的Efficientnet, 以及YOLO系列近期发出的最强的版本YOLOX, 都是在COCO数据集上作比较。而工业界都是根据各自的任务来选取或者采集相关的数据的。

一般来说, 数据处理(data processing)是对数据的采集、存储、查找、加工、变换和传输。根据处理设备的结构方式、工作方式, 以及数据的时间空间分布方式的不同, 数据处理有不同的方式。不同的处理方式要求不同的处理工具。每种处理方式都有自己的特点, 应当根据应用问题的实际环境选择合适的处理方式。

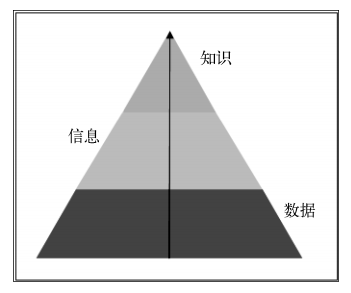
数据、信息与知识的关系如下图所示。这个过程是先从实验中收集数据, 再从数据中提取信息, 最后对信息进行细致的分析, 从中获取知识。
0

1. 数值处理

在数据的标准化方法中, 常用的有Batch Norm、Layer Norm、Instance Norm、Group Norm, 除此以外还有不太常用的Switchable Normalization、Filter Response Normalization

1.1 归一化

  • 区间缩放法(最大-最小标准化)
  • 二次型规范化

1.1.1 Min-Max 标准化(Min-Max Normalization)

也称为离差标准化, 是对原始数据的线性变换, 使结果值映射到\([0, 1]\)之间。转换函数如下：

\[ X^* = \frac{X-min}{max-min} \]

1.1.2 均值中心化(mean-centering)

就是通过与平均分的比较来决定一个评分为正或者为负。
中心化均值方法有个有趣的性质就是:用户对物品喜好倾向可以直接观察标准化后的评分值的正负情况。同时评分可以表示用户对物品喜好或厌恶的程度。

import pandas as pd
moive_matrix = {
    "John": {"The Matrix": 5, "Titanic":1, "Forrest Gump": 2, "Wall-E":2},
    "Lucy": {"The Matrix": 1, "Titanic":5, "Die Hard": 2, "Forrest Gump": 5, "Wall-E":5},
    "Eric": {"The Matrix": 2, "Die Hard": 3, "Forrest Gump": 5, "Wall-E": 4},
    "Diane": {"The Matrix": 4, "Titanic":3, "Die Hard": 5, "Forrest Gump": 3}
}
df = pd.DataFrame(moive_matrix).T

f = lambda x: x-x.mean()
print('________物品均值中心化________')
print(df.apply(f))
print('________用户均值中心化________')
print(df.apply(f, axis=1))

均值中心化方法移除来针对平均评分的不同感受而导致的偏差, 而Z-score标准化方法则考虑来个人评分范围不同带来的差异性。

1.1.3 Z-Score规范化

这种方法给予原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化。经过处理的数据符合标准正态分布, 即均值为 0, 标准差为 1, 转化函数为:

\[ X^* = \frac{X-\mu}{\sigma} \]

1.2 无量纲处理

无量纲化使不同规格的数据转换到同一规格, 常见的方法有: 标准化(Z-Score规范化)和区间缩放法(最大-最小标准化)、二次型规范化。
标准化的前提是特征值服从正态分布, 标准化后, 其转换成标准正态分布。区间缩放法利用了边界值信息, 将特征的取值区间缩放到某个特定的范围, 例如[0,1]等。

import numpy as np
from sklearn import preprocessing

x = np.array([
  [1., -1., 2.],
  [2., 0., 0.],
  [0., 1., -1.]
])
# 标准化(Z-Score规范化) x¹ = (x-x⁻)/S
x_scaled = preprocessing.scale(x)
print(x_scaled)

# 区间缩放法 x¹ = (x -Min) / (Max -Min)
x_max_min_scaled = preprocessing.MinMaxScaler().fit_transform(x)
print(x_max_min_scaled)

# 二次型规范化
x_normalize = preprocessing.normalize(x, norm='l2')
print(x_normalize)

1.3 非线性变换

常用的变换有基于多项式、基于指数函数和基于对数函数的变换等。一般对数变换后特征分布更平稳。对数变换能很好地解决随着自变量的增加, 因变量的方差增大的问题。另外一方面, 将非线性的数据通过对数变换, 转换为线性数据, 便于使用线性模型进行学习。

1.4 离散化

离散化后的特征对异常数据有很强的鲁棒性

  • 无监督离散化
    无监督的离散化方法通常为对特征进行装箱, 分为等宽度离散化方法和等频度离散化方法。等宽度离散方法, 就是根据箱的个数得出固定的宽度, 使得分到每个箱中的数据的宽度是相等的。等频分箱法是使得分到每个箱中的数据的个数是相同的。
    基于聚类分析的离散化方法也是一种无监督的离散化方法。

  • 有监督离散化
    有监督的离散化方法相较无监督的离散化方法拥有更多的表现形式及处理方式, 但目前比较常用的方法为基于熵的离散化方法和基于卡方的离散化方法。

熵是最常用的离散化度量之一。基于熵的离散化方法使用类分布信息计算和确定分裂点, 是一种有监督的、自顶向下的分裂技术。ID3 和 C4.5 是两种常用的使用熵的度量准则来建立决策树的算法, 基于这两种方法进行离散化特征儿乎与建立决策树的方法一致。在上述方法上又产生了 MDLP 方法(最小描述距离长度法则)

不同于基于熵的离散化方法, 基于卡方的离散化方法是采用自底向上的策略, 首先将数据取值范围内的所有数据值列为一个单独的区间, 再递归找出最佳邻近可合井的区间, 然后合并它们, 进而形成较大的区间。最常用的基于卡方的离散化方法是 ChiMerge 方法.

1.5 正则化

为了防止过拟合现象, 我们加入了正则化项, 常用的有 L1 范数和 L2范数。常用的向量的范数如下。

  • L0 范数: \(||x||0\) 为 x 向量各个非零元素的个数。
  • L1 范数: \(||x||1\) 为 x 向量各个元素绝对值之和, 也叫"稀疏规则算子"(Lasso Regularization)。
  • L2 范数: \(||x||2\) 为 x 向量各个元素平方和的 1/2 次方, L2 范数又称Euclidean 范数或者 Frobenius 范数。在回归里面, 有人把有它的回归叫"岭回归"(Ridge Regression), 有人也叫它"权值衰减(Weight Decay)"。
  • Lp 范数: \(||x||\)为 x 向量各个元素绝对值 p 次方和的 1/p 次方。
  • \(L\infty\)范数: \(||x||\)为 x 向量各个元素绝对值最大那个元素的绝对值。

常用的正则化项除了 L1 范数和 L2 范数外, 还有一种名为 Dropout 的方法。

2. 离散处理

2.1 One-Hot 编码

如果一个特征有m个可能值, 那么通过 One-Hot 编码后就变成了m个二元特征, 并且这些特征互斥。One-Hot 编码可以将离散特征的取值扩展到欧式空间, 离散特征的某个取值就是对应欧式空间的某个点, 可以方便在学习算法中进行相似度等计算, 并且可以稀疏表示, 减少存储, 同时可以一定程度上起到扩充特征的作用。

import numpy as np
from sklearn import preprocessing

one_hot_enc = preprocessing.OneHotEncoder()
one_hot_enc.fit([[1, 1, 2], [0, 1, 0], [0, 2, 1], [3, 0, 3]])
after_one_hot = one_hot_enc.transform([[3, 2, 3]]).toarray()
print(after_one_hot)

from sklearn import preprocessing
# 创建特征
feature = np.array([["Texas"], ["California"], ["Texas"], ["Delaware"], ["Texas"]])
# 创建 one-hot 编码器
one_hot = preprocessing.LabelBinarizer()
# 对特征进行 one-hot 编码
one_hot.fit_transform(feature)

# 创建能处理多个分类的 one-hot 编码器
one_hot_multiclass = MultiLabelBinarizer()

可能认为给每个分类赋予一个数值型的值是一个很不错的方法(比如, Texas=1, California=2), 但是由于这些分类没有内在的顺序(比如, 实际上Texas并不比California“小”), 使用数值就会错误地赋予分类一个并不存在的顺序。

正确的策略是为原特征中的每一个分类都创建一个二元特征。这个方法被称为one-hot编码(在机器学习的文献中)或者虚拟变量(在统计学的文献中)。

值得注意的是, 在 one-hot 编码之后, 最好从结果矩阵中删除一个 one-hot 编码的特征, 以避免线性依赖。

2.2 特征哈希

特征哈希法的目标是把原始的高维特征向量压缩成较低维特征向量, 且尽量不损失原始特征的表达能力, 是一种快速且很节省空间的特征向量化方法。

def hashing_vectorizer(s, N):
  x = [0 for i in range(N)]
  for f in s.split():
    h = hash(f)
    x[h % N] += 1
  return x

print(hashing_vectorizer('make a hash feature', 3))

2.3 时间特征处理

通常方案是按照业务逻辑以及业务目的进行相关特征的处理, Christ, M 等提出了一种层次化处理时间特征的方案, 其中包含了时间窗口统计特征: 最大、最小、均值、分位数, 并利用标签相关性对特征进行选择。

2.4 二值化

# 加载库
import numpy as np
from sklearn.preprocessing import Binarizer
# 创建特征
age = np.array([[6], [12], [20], [36], [65]])
# 创建二值化器
binarizer = Binarizer(threshold=18)
# 转换特征
binarizer.fit_transform(age)

2.5 根据多个阈值将数值型特征离散化

# 将特征离散化
np.digitize(age, bins=[20,30,64])

如果有足够的理由认为某个数值型特征应该被视为一个分类特征(categorical feature), 那么离散化会是一个卓有成效的策略。例如, 19岁和20岁的人消费习惯差距很小, 但是20岁和21岁(在美国, 21 岁的年轻人就可以饮酒了)的人之间消费习惯差距会很大。在这个例子中, 将人群划分成能喝酒的和不能喝酒的会很有用。同样, 在其他情况下, 将数据离散化为3个或更多区间也很有用。

3. 单变量

3.1 皮尔森相关系数

皮尔森相关系数是一种最简单的、能帮助理解特征和响应变量之间关系的方法, 该方法衡量的是变量之间的线性相关性, 结果的取值区间为[-1, 1], -1 表示完全的负相关(这个变量下降, 那个变量就会上升), +1 表示完全的正相关, 0 表示没有线性相关。
15

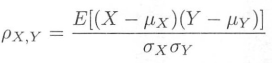
import numpy as np
from scipy.stats import pearsonr

np.random.seed(0)
size = 300
x = np.random.normal(0, 1, size)
print("Lower noise", pearsonr(x, x + np.random.normal(0, 1, size)))
print("Higher noise", pearsonr(x, x + np.random.normal(0, 10, size)))

3.2 距离相关系数

距离相关系数是为了克服皮尔森相关系数的弱点而产生的。它是基于距离协方差进行变量 间相关性度量, 它的一个优点为变量的大小不是必须一致的, 其计算方法如式 所示, 注意通常使用的值为其平方根:
16

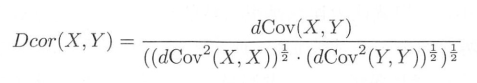
def dist(x, y):
    return np.abs(x[:, None] - y)

def d_n(x):
    d = dist(x, x)
    dn = d - d.mean(0) - d.mean(1)[:, None] + d.mean()
    return dn

def dcov_all(x, y):
    dnx = d_n(x)
    dny = d_n(y)
    
    denom = np.product(dnx.shape)
    dc = (dnx * dny).sum() / denom
    dvx = (dnx ** 2).sum() / denom
    dvy = (dny ** 2).sum() / denom
    dr = dc /(np.sqrt(dvx) * np.sqrt(dvy))
    return np.sqrt(dr)

x = np.random.uniform(-1, 1, 10000)
dc = dcov_all(x, x ** 2)
print(dc)

3.3 卡方检验

卡方检验最基本的思想就是通过观察实际值与理论值的偏差来确定理论的正确与否。

4. 数据标注

数据标注的工作一般是借助标注工具来完成的, 其中图像视频数据的标注工具又占了大部分, 常用的图像视频标注工具有labelme、labelbox、labelimg、精灵标注助手等工具, 值得一提的是精灵标注助手是一款非常强大的免费标注工具, 标注类型涵盖了图像数据、视频数据、语音数据、文本数据、3D点云数据, 而且适应目前主流的操作系统。

数据标注的类型包括了图像数据标注、视频数据标注、语音数据标注、文本数据标注、3D点云数据标注。标注的方式有人工标注、半自动标注、自动标注、众包等。具体选用哪种方式标注数据, 要看数据量和数据的类型, 有些通用数据是开源采样自动标注方法的, 比如使用训练好的人脸检测模型来标注人脸框的位置, 而有些特殊数据只能使用人工标注的方法。

4. 数据增强

数据增强方法一般分为光照变换、几何变换、遮挡变换、混合变换等。

  • 其中光照变换包括了随机亮度变换、对比度变换、色彩度变换、饱和度变换、噪声变换。
  • 几何变换包括了随机缩放、裁剪、翻转、旋转、平移等变换。
  • 遮挡变换包括了图像马赛克、随机图块删除等。主要方法有以下几种:Random erase, Cutout, hide and seek, Grid Mask, Dropblock

5. 异常数据

5.1 发现异常

5.1.1 查看所有观察值

与其说识别异常值(outlier)是一门技术, 不如说它是一门艺术。常用的方法是假设数据是正态分布的, 基于这个假设, 在数据周围“画”一个椭圆, 将所有处于椭圆内的观察值视为正常值(标注为 1), 将所有处于椭圆外的观察值视为异常值(标注为 -1)。

from sklearn.covariance import EllipticEnvelope
from sklearn.datasets import make_blobs

# 创建模拟数据
features, _ = make_blobs(n_samples = 10, n_features = 2, centers = 1, random_state = 1)
# 将第一个观察值的值替换为极端值
features[0,0] = 10000
features[0,1] = 10000
# 创建识别器
outlier_detector = EllipticEnvelope(contamination=.1)
# 拟合识别器
outlier_detector.fit(features)
# 预测异常值
outlier_detector.predict(features)

这个方法的一个主要限制是它需要指定一个 contamination(污染指数)参数, 表示异常值在观察值中的比例——这个值我们也不知道是多少。可以将 contamination视为你估计的数据的清洁程度。如果你认为数据中只有很少几个异常值, 可以将contamination 设置得小一点。反之, 如果数据中很有可能有好几个异常值, 就将contamination 设置为一个更大的值。

5.1.2 只查看某些特征

除了查看所有观察值, 我们还可以只查看某些特征, 并使用四分位差(interqutile range, IQR)来识别这些特征的极端值。

feature = features[:,0]
# 创建一个函数来返回异常值的下标
def indicies_of_outliers(x):
    q1, q3 = np.percentile(x, [25, 75])
    iqr = q3 - q1
    lower_bound = q1 - (iqr * 1.5)
    upper_bound = q3 + (iqr * 1.5)
    return np.where((x > upper_bound) | (x < lower_bound))
# 执行函数
indicies_of_outliers(feature)

IQR是数据集的第1个四分位数和第3个四分位数之差。可以将IQR视为数据集中大部分数据的延展距离, 而异常值会远远地偏离数据较为集中的区域。异常值常常被定义为比第1个四分位数小1.5 IQR(即IQR的1.5倍)的值, 或比第3个四分位数大1.5 IQR的值。

实际上没有一个通用的识别异常值的解决方案。每一种技术都有它的优点和缺点。最好的策略是尝试多种技术(比如EllipticEnvelope和基于IQR的识别)并从整体上来看结果。
如果可能的话, 你应该仔细看一看被识别为异常值的观察值, 并尝试去解释它们。

5.2 处理异常值

  • 丢弃
  • 标记为异常值
  • 对有异常值的特征进行转换
  • 删除缺失值
  • 填充缺失值: 可以使用KNN(K-Nearest Neighbors, K近邻)算法来预测缺失值, 还可以使用scikit-learn的 Imputer模块, 用特征的平均值、中位数或者众数来填充缺失值, 不过效果通常都会比使用 KNN 的差
houses["Log_Of_Square_Feet"] = [np.log(x) for x in houses["Square_Feet"]]

# 创建特征矩阵
features = np.array([[1.1, 11.1],
  [2.2, 22.2],
  [3.3, 33.3],
  [4.4, 44.4],
  [np.nan, 55]])
# 只保留没有(用 ~ 来表示)缺失值的观察值
features[~np.isnan(features).any(axis=1)]

dataframe.dropna()

KNN

import numpy as np
from fancyimpute import KNN
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_blobs

# 创建模拟特征矩阵
features, _ = make_blobs(n_samples = 1000, n_features = 2, random_state = 1)
# 标准化特征
scaler = StandardScaler()
standardized_features = scaler.fit_transform(features)
# 将第一个特征向量的第一个值替换为缺失值
true_value = standardized_features[0,0]
standardized_features[0,0] = np.nan
# 预测特征矩阵中的缺失值
features_knn_imputed = KNN(k=5, verbose=0).complete(standardized_features)
# 对比真实值和填充值
print("True Value:", true_value)
print("Imputed Value:", features_knn_imputed[0,0])

from sklearn.preprocessing import Imputer
# 创建填充器
mean_imputer = Imputer(strategy="mean", axis=0)
# 填充缺失值
features_mean_imputed = mean_imputer.fit_transform(features)
# 对比真实值和填充值
print("True Value:", true_value)
print("Imputed Value:", features_mean_imputed[0,0])

和识别异常值一样, 处理异常值时也不存在一个绝对准则。应该基于两个方面来考虑对异常值的处理。第一, 要弄清楚是什么让它们成为异常值的。如果你认为它们是错误的观察值, 比如它们来自一个坏掉的传感器或者是被记错了的值, 那么就要丢弃它们或者用 NaN 来替换异常值, 因为我们无法信任这些值。但是, 如果你认为这些异常值真的就是极端值(例如一幢大宅子有 200 间卧室), 那么把它们标记为异常值或者对它们的值进行转换, 是更合理的做法。

对于异常值到底要如何处理呢？首先, 想一想它们为什么是异常值, 然后对于数据要有一个最终的目标。最重要的是, 要记住“决定不处理异常值”本身就是一个有潜在影响的决定。

另外, 如果数据中有异常值, 那么采用标准化方法做缩放就不太合适了, 因为平均值和方差受异常值的影响很大。这种情况下, 需要针对异常值使用一个鲁棒性更高的缩放方法, 比如 RobustScaler。

删除带缺失值的观察值也是一件令人心痛的决定。这样做会让算法丢失观察值中那些非缺失值的信息, 所以删除观察值只能作为最终别无他法时不得已的选择。还有一点很重要, 删除观察值可能会在数据中引入偏差, 这主要由缺失值的成因决定。

  • 完全随机缺失(Missing Completely At Random, MCAR)
  • 随机缺失(Missing At Random, MAR)
  • 完全非随机缺失(Missing Not At Random, MNAR)

6. 文本数据

大多数文本数据在被用于生成特征之前都需要进行清洗。Python 的标准字符串操作能完成大部分基本的文本清洗操作。在现实场景中, 我们通常需要自定义清洗函数(比如, capitalizer)完成一些组合的清洗任务, 再将该函数应用于文本数据。

  • 清洗

  • 解析
    Beautiful Soup是一个可以从HTML或XML文件中提取数据的Python库, 提供了很多选项。

  • 移除标点
    translate 因其非凡的性能成为 Python 中非常流行的函数。

  • 文本分词
    Python 的自然语言工具集(Natural Language Toolkit, NLTK)在处理文本方面有很多功能强大的操作, 其中包括文本分词(word tokenizing)。
    文本分词, 尤其是将文本分为独立的单词是在清洗文本数据之后的常见任务, 因为它是将文本转换成能用于构建有效特征的数据的第一步。

  • 删除停用词
    尽管“停止词”可以指代所有需要在数据预处理阶段删除的单词, 但是这个术语常常用来指代那些特别常见而包含的信息又很少的单词。

  • 提取词干

  • 标注词性
    NLTK使用Penn Treebank的词性标签进行标注。

  • 文本编码成词袋
    将文本转换成特征的最常用的方法之一就是使用词袋模型(bag-of-words model)。词袋模型为文本数据中的每一个单词都输出一个特征, 每个特征都包含该单词在观察值中出现的次数。

  • 按单词的重要性加权
    使用 TF-IDF(term frequency-inverse document frequency)将一个词在某个文档(推文、影评、演讲稿等)中的出现次数和这个词在所有文档中的出现次数进行对比。用scikit-learn的TfidfVectorizer能很方便地做这个对比。

7. 开源数据集

参考:
三种识别异常值的方法
使用 one-hot 编码的时候需要删除一列


Copyright © 2025 iawen.com All rights reserved.  粤ICP备12068889号-1