目录

• • 1. 简介
    • 1.1 使用NumPy的操作
    • 1.2 NumPy - MatLab的替代品
    • 1.3 性能
  • 2. 基本知识
    • 2.1 NumPy Ndarray对象
      • 2.1.1 稀疏矩阵
    • 2.2 数据类型对象(dtype)
    • 2.3 数组属性
    • 2.4 数组创建
    • 2.5 索引和切片
    • 2.6 高级索引
      • 2.6.1 整数索引
      • 2.6.2 布尔数组索引
    • 2.7 复制和视图
    • 2.8 输入/输出
  • 3. 高级操作
    • 3.1 广播
    • 3.2 遍历数组
      • 3.2.1 参数op_flags
      • 3.2.2 参数flags
    • 3.3 其他
      • 3.3.1 矩阵的秩
      • 3.3.2 行列式
      • 3.3.3 矩阵的对角线元素
      • 3.3.4 矩阵的迹
      • 3.3.5 特征值和特征向量
      • 3.3.5 矩阵的逆
  • 4. 数组操作
    • 4.1 改变形状
    • 4.2 转置操作
    • 4.3 改变尺寸
    • 4.4 合并数组
    • 4.5 分割数组
    • 4.6 添加/删除元素
    • 4.7 其他
  • 5. 二进制运算
  • 6. 字符串运算
  • 7. 数学函数
    • 7.1 三角函数
    • 7.2 Rounding函数
    • 7.3 算术操作
  • 8. 矩阵库
  • 9. 线性代数
    • 10.1 Poly1d
  • 10. 与Matplotlib结合
    • 10.1 格式化字符
    • 10.2 颜色缩写定义|
    • 10.3 其他绘图函数

NumPy是一个Python包。它代表着"Numerical Python"(数值Python)。它是一个由多维数组对象和一系列用于处理数组的例程组成的库。
NumPy是Python机器学习技术栈的基础。NumPy能对机器学习中常用的数据结构——向量(vector)、矩阵(matrice)、张量(tensor)——进行高效的操作。

1. 简介

Numeric是NumPy的前身, 由Jim Hugunin开发。还开发了另一个包Numarray, 具有一些额外的功能。2005年, Travis Oliphant将Numarray的特性合并到Numeric包中创建了NumPy包。这个开源项目有许多贡献者。

1.1 使用NumPy的操作

• 对数组进行数学和逻辑运算。
• 傅里叶变换和形状操作的例程。
• 与线性代数相关的操作。NumPy具有内置的线性代数和随机数生成函数。

1.2 NumPy - MatLab的替代品

NumPy通常与SciPy(科学Python)和Mat-plotlib(绘图库)等包一起使用。这个组合被广泛用作MatLab的替代品, MatLab是一个流行的技术计算平台。然而, Python作为MatLab的替代方案现在被认为是一种更现代和完整的编程语言。

1.3 性能

Python的标量计算比Numpy的标量计算要快。对于仅包含一两个元素的操作Python标量比Numpy的数组要快。但是当数组稍微大一点时Numpy就会胜出了。

一般情况下OpenCV的函数要比Numpy函数快。所以对于相同的操作最好使用OpenCV的函数。当然也有例外, 尤其是当使用Numpy对视图(而非复制)进行操作时。

2. 基本知识

2.1 NumPy Ndarray对象

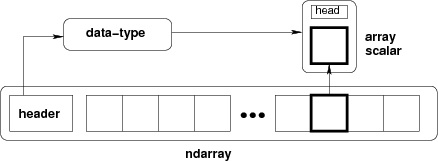
NumPy中定义的最重要的对象是一个被称为ndarray的N维数组类型。它描述了一组相同类型的项目。可以使用零为基础的索引来访问集合中的项目。ndarray中的每个项目在内存中占用相同大小的块。ndarray中的每个元素都是一个数据类型对象的对象(称为dtype)。

通过切片从ndarray对象中提取的任何项目都由一个数组标量类型的Python对象表示。以下图表显示了ndarray、数据类型对象(dtype)和数组标量类型之间的关系。

numpy.array(object, dtype = None, copy = True, order = None, subok = False, ndmin = 0)

ndarray对象由计算机内存中的一个连续的一维段组成, 结合一个索引方案, 将每个项目映射到内存块中的位置。内存块按行主序(C风格)或列主序(FORTRAN或MatLab风格)存储元素。

vector_row = np.array([1, 2, 3])
vector_column = np.array([[1],[2],[3]])

matrix = np.array([[1, 2],
  [1, 3],
  [1, 4]])

matrix_object = np.mat([[1, 2],
    [1, 3],
    [1, 4]])

z[:2,:]

不推荐使用矩阵数据结构(np.mat)。有两个原因，一是实际上数组才是NumPy的标准数据结构，二是绝大多数NumPy操作返回的是数组而不是矩阵对象。

2.1.1 稀疏矩阵

稀疏矩阵只保存非零元素并假设剩余元素的值都是零，这样能节省大量的计算成本。稀疏矩阵的类型有很多，比如，压缩的稀疏列、表中表以及键值对词典。

import numpy as np
from scipy import sparse

matrix = np.array([[0, 0], [0, 1], [3, 0]])
matrix_sparse = sparse.csr_matrix(matrix)

2.2 数据类型对象(dtype)

数据类型对象描述了对应于数组的固定存储区块的解释方式, 具体取决于以下方面:

• 数据的类型(整型、浮点型或Python对象)
• 数据的大小
• 字节序(小端或大端): 字节序可以通过在数据类型前加上’<‘或’>‘来决定。’<‘表示编码为小端序(最低有效位存储在最小地址), ‘>‘表示编码为大端序(最高有效字节存储在最小地址)。
• 对于结构化类型, 字段名、每个字段的数据类型以及每个字段占用的存储区块的一部分
• 如果数据类型是一个子数组, 它的形状和数据类型

numpy.dtype(object, align, copy)

• Object - 需要转换为对象数据类型的对象
• Align - 如果为True, 则对字段添加填充, 使其类似于C-struct
• Copy - 创建dtype对象的新副本。如果为False, 结果是内建数据类型对象的引用

int8, int16, int32, int64 can be replaced by equivalent string ‘i1’, ‘i2’,‘i4’, etc.

import numpy as np 

dt = np.dtype('i4')
print(dt)

每个内置数据类型都有一个字符代码, 用于唯一标识它。

• ‘b’ - 布尔型数据
• ‘i’ - (有符号)整型数据
• ‘u’ - 无符号整型数据
• ‘f’ - 浮点型数据
• ‘c’ - 复数浮点型数据
• ’m’ - 时间间隔数据
• ‘M’ - 日期时间数据
• ‘O’ - (Python)对象数据
• ‘S’, ‘a’ - (字节)字符串数据
• ‘U’ - Unicode 数据
• ‘V’ - 原始数据(空类型)

2.3 数组属性

• ndarray.shape: 该数组属性返回一个元组, 表示数组的维度。它还可以用于调整数组的大小。
• ndarray.ndim: 这个数组属性返回数组的维度数量。
• numpy.size
• numpy.itemsize: 此数组属性返回数组的每个元素的字节长度。
• numpy.flags:
  • C_CONTIGUOUS (C) 数据在一个C风格的连续段中
  • F_CONTIGUOUS (F) 数据在一个Fortran风格的连续段中
  • OWNDATA (O) 数组拥有它使用的内存, 或者从另一个对象借用内存
  • WRITEABLE (W) 数据区可以被写入。将其设置为False会锁定数据, 使其只读
  • ALIGNED (A) 数据和所有元素对硬件适当地对齐
  • UPDATEIFCOPY (U) 此数组是另一个数组的副本。当释放此数组时, 基础数组将使用此数组的内容进行更新

2.4 数组创建

• numpy.empty: 创建一个指定形状和dtype的未初始化数组, numpy.empty(shape, dtype = float, order = 'C')
• numpy.zeros: 返回一个指定大小的新数组, 填充为零, numpy.zeros(shape, dtype = float, order = 'C')
• numpy.ones: 返回一个指定大小和类型的新数组, 填充为1, numpy.ones(shape, dtype = None, order = 'C')
• numpy.asarray: 此函数类似于numpy.array, 但参数较少。此例程可用于将Python序列转换为ndarray, numpy.asarray(a, dtype = None, order = None)
• numpy.frombuffer: 此函数将一个缓冲区解释为一维数组。将任何公开缓冲区接口的对象作为参数返回一个 ndrray 。

numpy.frombuffer(buffer, dtype = float, count = -1, offset = 0)

• numpy.fromiter: 这个函数从任何可迭代对象中构建一个 ndarray 对象。该函数返回一个新的一维数组。

numpy.fromiter(iterable, dtype, count = -1)

• numpy.arange: 返回一个ndarray对象, 其中包含在给定范围内均匀分布的值。格式如: numpy.arange(start, stop, step, dtype)
• numpy.linspace: 类似于arange()函数。在这个函数中, 不需要指定步长, 而是指定间隔之间均匀间隔的值的数量。用法如: numpy.linspace(start, stop, num, endpoint, retstep, dtype)
• numpy.logspace: 返回一个 ndarray 对象, 其中包含在对数刻度上均匀间隔的数字。刻度的起点和终点是基数的指数, 通常为10。

numpy.logspace(start, stop, num, endpoint, base, dtype)

• numpy.random: 生成随机数

# 设置随机数种子
np.random.seed(0)

# 生成 3 个 0.0 到 1.0 之间的随机浮点数
np.random.random(3)
# array([ 0.5488135 , 0.71518937, 0.60276338])

# 生成 3 个 1 到 10 之间的随机整数
np.random.randint(0, 11, 3)

# 从平均值是 0.0 且标准差是 1.0 的正态分布中抽取 3 个数
np.random.normal(0.0, 1.0, 3)

# 从平均值是 0.0 且散布程度是 1.0 的 logistic 分布中抽取 3 个数
np.random.logistic(0.0, 1.0, 3)

# 从大于或等于 1.0 并且小于 2.0 的范围中抽取 3 个数
np.random.uniform(1.0, 2.0, 3)

2.5 索引和切片

可以通过索引或切片来访问和修改ndarray对象的内容, 就像Python的内置容器对象一样。
基本切片是Python基本切片概念在n维度中的扩展。Python切片对象可通过将 start、stop 和 step 参数传递给内置 slice 函数来构建。这个切片对象被传递给数组以提取数组的一部分。

import numpy as np

a = np.arange(10) 
b = a[2:7:2] 
print(b)

切片也可以包含省略号(…)以使选择元组的长度与数组的维度相同。如果在行位置使用省略号, 则返回一个由行中的项组成的ndarray。

import numpy as np 
a = np.array([[1,2,3],[3,4,5],[4,5,6]]) 

print(a[...,1])
print(a[1,...])
print(a[...,1:])

2.6 高级索引

可以从ndarray中进行选择, 该ndarray是一个非元组序列、整数或布尔数据类型的ndarray对象, 或者一个至少包含一个序列对象的元组。高级索引总是返回数据的副本。相比之下, 切片只呈现一个视图。

2.6.1 整数索引

可以根据其N维索引在数组中选择任意项。每个整数数组表示该维度的索引数。当索引包含与目标ndarray的维度一样多的整数数组时, 它变得简单直接。

import numpy as np 

x = np.array([[1, 2], [3, 4], [5, 6]]) 

# 选择包括来自第一个数组的(0,0)、(1,1)和(2,0)位置上的元素。
y = x[[0,1,2], [0,1,0]] 
print(y)

2.6.2 布尔数组索引

当期望的结果是布尔操作(比如比较运算符)的结果时, 使用这种高级索引。

import numpy as np 

a = np.array([np.nan, 1,2,np.nan,3,4,5]) 
print(a[~np.isnan(a)])

2.7 复制和视图

在执行函数时, 其中一些函数会返回输入数组的副本, 而其他一些函数会返回视图。当内容在另一个位置物理存储时, 称为 复制 。另一方面, 如果提供了相同内存内容的不同视图, 我们称之为视图。
简单的赋值不会创建数组对象的副本。相反, 它使用原始数组的相同id()来访问它。id()返回Python对象的通用标识符, 类似于C中的指针。
此外, 任何一方的更改都会反映在另一方上。例如, 一个的形状改变, 另一个的形状也会改变。

NumPy有一个名为ndarray.view()的方法, 它是一个查看原始数组相同数据的新数组对象。与之前的情况不同, 新数组的维度的变化不会改变原始数组的维度。

ndarray.copy()函数创建一个深拷贝。它是数组和其数据的完全复制, 并且不与原始数组共享。

2.8 输入/输出

NumPy引入了一种简单的ndarray对象文件格式。该 .npy 文件存储了在磁盘文件中重构ndarray所需的数据、形状、数据类型和其他信息, 以便即使文件在具有不同体系结构的另一台机器上, 也可以正确地检索该数组。

ndarray对象可以保存到磁盘文件中, 并从磁盘文件中加载。可用的IO函数如下:

• load() 和 save() 函数用于处理NumPy二进制文件(扩展名为.npy)
• loadtxt() 和 savetxt() 函数用于处理普通文本文件

3. 高级操作

3.1 广播

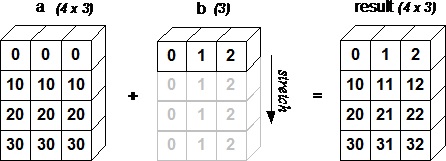
术语 broadcasting 指的是NumPy在算术运算过程中能够处理不同形状的数组的能力。数组的算术运算通常是对应元素进行操作。如果两个数组正好具有相同的形状, 则这些运算能够顺利进行。
如果两个数组的维度不相似, 就无法进行元素对元素操作。然而, 在NumPy中, 可以对非相似形状的数组进行操作, 这是因为它具备了广播功能。较小的数组将被 广播 到较大数组的大小, 以使它们具有兼容的形状。

如果满足以下规则, 则可以进行广播:

• 具有较小ndim的数组, 在其形状中以'1’作为前缀。
• 输出形状的每个维度的大小是该维度中输入大小的最大值。
• 如果输入在特定维度上的大小与输出大小匹配, 或者其值恰好为1, 则可以在计算中使用输入。
• 如果输入的维度大小为1, 则在该维度上的所有计算中都使用该维度的第一个数据条目。

如果满足上述规则并且以下条件之一成立, 则一组数组被称为 可广播的:

• 数组具有完全相同的形状。
• 数组具有相同数量的维度, 并且每个维度的长度是一个共同的长度或1。
• 维度较少的数组可以在其形状上增加一个长度为1的维度, 以使上述属性成立。

3.2 遍历数组

NumPy包含一个迭代器对象numpy.nditer。它是一个高效的多维迭代器对象, 可以用来迭代访问数组。使用Python的标准迭代器接口, 可以访问数组的每个元素。

import numpy as np

a = np.arange(0,60,5)
a = a.reshape(3,4)

for x in np.nditer(a):
   print(x)

迭代的顺序被选择为与数组的内存布局匹配, 而不考虑特定的排序。如果相同的元素使用F-style顺序存储, 则迭代器会选择更高效的遍历数组的方式。可以通过明确指定的方式来强制使用特定顺序的nditer对象。

3.2.1 参数op_flags

nditer对象还有一个可选的参数叫做op_flags。它的默认值是只读的, 但可以设置为读写或者只写模式。这将允许使用这个迭代器来修改数组元素。

import numpy as np
a = np.arange(0,60,5)
a = a.reshape(3,4)

for x in np.nditer(a, op_flags = ['readwrite']):
   x[...] = 2*x

print(a)

3.2.2 参数flags

flags参数, 可以取以下值:

• c_index: 可以追踪C_order索引
• f_index: 可以追踪Fortran_order索引
• multi-index: 可以追踪每次迭代的索引类型
• external_loop: 导致给出的值为多个值的一维数组, 而不是零维数组

如果两个数组是可广播的, 组合的nditer对象能够同时迭代它们。假设一个数组a有尺寸为3×4, 还有另一个尺寸为1×4的数组b, 则使用以下类型的迭代器(数组b被广播到a的尺寸)。

import numpy as np 
a = np.arange(0,60,5) 
a = a.reshape(3,4) 
b = np.array([1, 2, 3, 4], dtype = int) 

for x, y in np.nditer([a,b]): 
   print("%d:%d" % (x,y))

3.3 其他

3.3.1 矩阵的秩

矩阵的秩就是由它的列或行展开的向量空间的维数。使用 NumPy 中的线性代数方法 matrix_rank。

# 创建一个矩阵
matrix = np.array([[1, 1, 1],
[1, 1, 10],
[1, 1, 15]])

# 返回矩阵的秩
np.linalg.matrix_rank(matrix)
# 2

3.3.2 行列式

矩阵的行列式是很有用的，使用 NumPy 的 det 能很容易地计算出矩阵的行列式。
行列式在线性代数中是一个非常有用的值。它通过对角元素计算得来, 而对于一个二阶矩阵来说, 它就是左上角元素与右下角元素的乘积减去其他两个元素的乘积。换句话说, 对于一个矩阵\([[a,b], [c,d]]\), 行列式的计算公式为’ad-bc’。而更大的方阵被看作是\(2\times2\)矩阵的组合。

matrix = np.array([[1, 2, 3],
[2, 4, 6],
[3, 8, 9]])

# 返回矩阵的行列式
np.linalg.det(matrix)
# 0.0

3.3.3 矩阵的对角线元素

使用 NumPy 的 diagonal 很容易获取矩阵的对角线元素。我们还可以使用 offset 参数在主对角线的上下偏移，获取偏移后的对角线方向的元素。

# 创建一个矩阵
matrix = np.array([[1, 2, 3],
[2, 4, 6],
[3, 8, 9]])

# 返回对角线元素
matrix.diagonal()
# array([1, 4, 9])

3.3.4 矩阵的迹

矩阵的迹是其对角线元素之和，常被用在机器学习方法的底层计算中。给定一个 NumPy的多维数组，使用 trace 就能计算出它的迹。我们还可以通过先返回矩阵的对角线元素再对其求和的方式来计算矩阵的迹。

# 创建一个矩阵
matrix = np.array([[1, 2, 3],
[2, 4, 6],
[3, 8, 9]]),

# 返回矩阵的迹
matrix.trace()
# 14

3.3.5 特征值和特征向量

在机器学习库中，特征向量被广泛地使用。从直觉上来说，假设线性变换是以矩阵\(A\)的形式给出的，则当应用此线性变换时，特征向量只会改变大小（不改变方向）。更正式的描述如下 ：

\(A\)是方阵，\(\lambda\) 为特征值， \(v\)为特征向量。在 NumPy 的线性代数工具集中， eig 能计算出任何方阵的特征值和特征向量。

# 创建一个矩阵
matrix = np.array([[1, -1, 3],
[1, 1, 6],
[3, 8, 9]])

# 计算特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(matrix)
eigenvalues, eigenvectors
# (array([13.55075847,  0.74003145, -3.29078992]),
#  array([[-0.17622017, -0.96677403, -0.53373322],
#         [-0.435951  ,  0.2053623 , -0.64324848],
#         [-0.88254925,  0.15223105,  0.54896288]]))

3.3.5 矩阵的逆

假设方阵 \(A\) 的逆是另一个矩阵\(A^{-1}\)，则 ：

I 是单位矩阵。如果 A-1 存在，则可以使用 NumPy 的 linalg.inv 来计算。为了看到效果，可以将一个矩阵和它的逆矩阵相乘，结果会是一个单位矩阵。

# 创建一个矩阵
matrix = np.array([[1, 4], [2, 5]])
# 计算一个矩阵的逆
np.linalg.inv(matrix)
# array([[-1.66666667,  1.33333333],
#        [ 0.66666667, -0.33333333]])

matrix @ np.linalg.inv(matrix)
# array([[1.00000000e+00, 0.00000000e+00],
#        [1.11022302e-16, 1.00000000e+00]])

4. 数组操作

NumPy包中有几个例程可用于操作ndarray对象中的元素。它们可以分为以下几类:

• 改变形状
• 转置操作
• 改变尺寸
• 合并数组
• 分割数组
• 添加/删除元素

4.1 改变形状

• numpy.reshape: 可以改变数组的形状, 但不改变数据。它接受以下参数: numpy.reshape(arr, newshape, order)
  新形状应与原始形状兼容

matrix = np.array([[1, 2, 3],
    [4, 5, 6],
    [7, 8, 9],
    [10, 11, 12]])
matrix.reshape(2, 6)
# array([[ 1,  2,  3,  4,  5,  6],
#        [ 7,  8,  9, 10, 11, 12]])

• numpy.ndarray.flat: 返回数组的一个1-D迭代器。其表现类似于Python的内置迭代器。
• numpy.ndarray.flatten: 返回将数组折叠到一维的副本。flatten是将矩阵转换成一维数组的一种简单方法。另一种方法是使用 reshape来创建一个行向量。

matrix = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
matrix.flatten()
# array([1, 2, 3, 4, 5, 6, 7, 8, 9])

matrix.reshape(1, -1)
# array([[1, 2, 3, 4, 5, 6, 7, 8, 9]])

• numpy.ravel: 返回一个展平的一维数组。只在需要时才会进行复制。返回的数组将具有与输入数组相同的类型。numpy.ravel(a, order)
  order ‘C’: 行优先顺序(默认) ‘F’: 列优先顺序 ‘A’: 按列优先顺序展开, 如果a在内存中是Fortran连续的, 则按行优先顺序展开, 否则按内存中元素出现的顺序展开’K’: 按照元素出现在内存中的顺序展开a

4.2 转置操作

• numpy.transpose: 对给定的数组进行维度重排。它尽可能地返回视图。numpy.transpose(arr, axes)
  axes 整数列表, 对应维度。默认情况下, 维度是反转的
• numpy.ndarray.T: 它的行为类似于numpy.transpose。
  转置在线性代数中是很常见的操作，它将每个元素的行、列下标互换。在线性代数范围外有一点常被忽视 ：严格来说一个向量是不能被转置的，因为它只是值的集合。

matrix = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
matrix.T

np.array([1, 2, 3, 4, 5, 6]).T
np.array([[1, 2, 3, 4, 5, 6]]).T

• numpy.rollaxis: 将指定的轴向后滚动, 直到它位于指定的位置。numpy.rollaxis(arr, axis, start)
• numpy.swapaxes: 交换数组的两个轴。对于1.10之后的NumPy版本, 将返回交换后数组的视图。numpy.swapaxes(arr, axis1, axis2)

4.3 改变尺寸

• numpy.broadcast: 模拟广播机制。它返回一个封装了将一个数组广播到另一个数组的结果的对象。
• numpy.broadcast_to: 将一个数组广播到新的形状。它返回原始数组的只读视图。它通常不是连续的。如果新形状不符合NumPy的广播规则, 该函数可能会引发ValueError。numpy.broadcast_to(array, shape, subok)
• numpy.expand_dims: 扩通过在指定位置插入一个新轴来扩展数组。numpy.expand_dims(arr, axis)
• numpy.squeeze: 从给定数组的形状中去除一维条目。numpy.squeeze(arr, axis)

4.4 合并数组

• numpy.concatenate: 用于沿指定轴将两个或多个具有相同形状的数组连接起来。numpy.concatenate((a1, a2, ...), axis)
• numpy.stack: 沿着一个新轴连接数组序列。此函数自NumPy版本1.10.0起增加。numpy.stack(arrays, axis)
• numpy.hstack: 用于将数组水平堆叠在一起以形成一个单一的数组。
• numpy.vstack: 用于垂直堆叠数组以形成一个单一数组。

4.5 分割数组

• numpy.split: 沿着指定的轴将数组分割成子数组。numpy.split(ary, indices_or_sections, axis)
• numpy.hsplit: 是split()函数的一个特殊情况, 其中axis为1表示无论输入数组的维度如何, 都将进行水平拆分。
• numpy.vsplit: 是split()函数的一种特殊情况, 其中axis为1, 表示无论输入数组的维度如何, 都进行垂直拆分。

4.6 添加/删除元素

• numpy.resize: 返回一个指定大小的新数组。如果新尺寸大于原始尺寸, 则原始数组的条目将被重复复制。numpy.resize(arr, shape)
• numpy.append: 在输入数组的末尾添加值。 追加操作不是就地执行的, 而是分配一个新的数组。 此外, 输入数组的维度必须匹配, 否则将引发 ValueError。numpy.append(arr, values, axis)
• numpy.insert: 沿着给定的轴在输入数组中的给定索引之前插入值。如果要插入的值的类型与输入数组不同, 将进行类型转换。插入操作不会在原地进行, 并且该函数会返回一个新数组。另外, 如果未提及轴, 则会对输入数组进行扁平化处理。numpy.insert(arr, obj, values, axis)
• numpy.delete: 从输入数组中删除指定的子数组, 并返回一个新数组。与insert()函数一样, 如果未使用axis参数, 则输入数组会被展平。numpy.delete(arr, obj, axis)
• numpy.unique: 返回输入数组中唯一元素的数组。该函数能够返回一个包含唯一值数组和关联索引数组的元组。索引的性质取决于函数调用中返回参数的类型。numpy.unique(arr, return_index, return_inverse, return_counts)

4.7 其他

• numpy.vecotrize: 将一个函数转换成另一个函数，这个函数能把某个操作应用在数组的全部元素或一个切片上。

matrix = np.array([[1, 2],
    [1, 2],
    [1, 2]])

add_100 = lambda i: i + 100
vectorized_add_100 = np.vectorize(add_100)
matrix2 = vectorized_add_100(matrix)

• numpy.max(matrix, axis=None)/numpy.min(matrix, axis=None): 元素的最大值和最小值, 而使用 axis 参数则可以对一个特定的坐标轴应用此操作

5. 二进制运算

• np.bitwise_and(): 位与运算
• np.bitwise_or(): 位或运算
• numpy.invert(): 按位NOT

print(np.invert(np.array([13], dtype = np.uint8))) 
print(np.binary_repr(13, width = 8))
print(np.binary_repr(242, width = 8))

• numpy.left_shift(): 左移运算
• numpy.right_shift(): 右移运算

6. 字符串运算

用于对dtype为numpy.string_或numpy.unicode_的数组执行矢量化字符串操作。它们基于Python内置库中的标准字符串函数。这些功能在字符数组类(numpy.char)中定义。较旧的Numarray包中包含了chararray类。numpy.char类中的上述功能在执行向量化字符串操作时非常有用。

• numpy.char.add(): 执行逐元素的字符串拼接。
• numpy.char.multiply(): 以元素级别返回多次连接的字符串
• numpy.char.center(): 返回所需宽度的数组, 使得输入字符串在左右两侧居中且填充 fillchar 。
• numpy.char.capitalize(): 返回仅首字母大写的字符串的副本
• numpy.char.title(): 返回输入字符串的标题格式版本, 每个单词的第一个字母都是大写的。
• numpy.char.lower(): 返回一个将元素转换为小写的数组。它会对每个元素调用 str.lower。
• numpy.char.upper(): 在数组中的每个元素上调用 str.upper 函数, 以返回大写的数组元素。
• numpy.char.split(): 返回输入字符串中的单词列表。默认情况下, 使用空格作为分隔符。否则, 指定的分隔符字符用于拆分字符串。
• numpy.char.splitlines(): 返回数组中的元素列表, 以行边界进行分割。
• numpy.char.strip(): 返回被指定字符剥离前导和/或尾随的数组副本。
• numpy.char.join(): 返回一个字符串, 其中的每个字符都由指定的分隔符字符连接在一起。
• numpy.char.replace(): 返回输入字符串的一个新副本, 其中所有字符序列的出现都被另一个给定的序列替换。
• numpy.char.decode(): 使用指定的编解码器对给定的字符串进行解码。
• numpy.char.encode(): 在数组中的每个元素上调用str.encode函数。默认编码为utf_8, 可以使用标准Python库中的编解码器。

7. 数学函数

7.1 三角函数

• np.sin()
• np.cos()
• np.tan()
• arcsin, arcos, 和 arctan 函数返回给定角度的正弦、余弦和正切的三角反函数。这些函数的结果可以通过将弧度转换为度数来验证 numpy.degrees()函数 。

7.2 Rounding函数

• numpy.around(): 返回按照指定精度四舍五入的值。
• numpy.floor(): 返回不大于输入参数的最大整数。标量 x 的向下取整是指最大的整数 i, 满足 i <= x。
• numpy.ceil(): 返回输入值的上限, 即标量x的上限是最小的整数i, 使得i >= x。

7.3 算术操作

• 执行诸如add(), subtract(), multiply()和divide()等算术操作的输入数组必须具有相同的形状或符合数组广播规则。

• numpy.reciprocal(): 返回参数的倒数, 元素级别计算。对于绝对值大于1的元素, 由于Python处理整数除法的方式, 结果始终为0。对于整数0, 会发出溢出警告。

• numpy.power(): 将第一个输入数组中的元素视为底数, 并将其乘以第二个输入数组中相应元素的幂次方。

• numpy.mod(): 返回输入数组中对应元素相除后的余数。函数 numpy.remainder() 也可以产生相同的结果。

• 对复数数组进行操作

  • numpy.real(): 返回复数数据类型参数的实部。
  • numpy.imag(): 返回复数数据类型参数的虚部。
  • numpy.conj(): 返回复数的共轭, 通过改变虚部的符号获得。
  • numpy.angle(): 返回复数参数的角度。该函数有一个degree参数。如果为真, 则返回角度为度数, 否则角度为弧度。

• 统计函数

  • numpy.amin()和numpy.amax(): 返回给定数组中指定轴的元素的最小值和最大值。
  • numpy.ptp(): 返回沿轴的值的范围(最大值-最小值)。
  • numpy.percentile(): 百分位数(或百分位数)是统计学中一个用来指示在一组观察值中, 有多少百分比观察值落在某个值以下的度量标准。numpy.percentile(a, q, axis)
  • numpy.median(): 被定义为将数据样本的上半部分和下半部分分开的值。
  • numpy.mean(): 算术平均数是沿着一个轴的元素的总和除以元素的数量。numpy.mean()函数返回数组中元素的算术平均数。如果提及了轴, 则沿着该轴计算。
  • numpy.average(): 加权平均值是通过将每个分量乘以反映其重要性的因子来计算的平均值。numpy.average()函数根据另一个数组中给定的权重, 计算数组中元素的加权平均值。该函数可以有一个轴参数。如果未指定轴, 则数组被展平。
  • np.std(): 标准差是平均偏差的平方根。标准差的公式如下: std = sqrt(mean(abs(x - x.mean())**2))
  • np.var(): Variance是平方差的平均值, 即 mean(abs(x - x.mean())2)** 。换句话说, 标准差是方差的平方根。

• 排序、搜索和计数函数

  • numpy.sort(a, axis, kind, order): kind 默认为快速排序。
  • numpy.argsort(): 在输入数组上执行间接排序, 沿给定轴使用指定的排序方式, 返回数据的索引数组。这个索引数组被用来构建排序后的数组。
  • numpy.lexsort(): 使用键序列进行间接排序。可以将这些键看作是电子表格中的一列。函数返回一个索引数组, 可以使用该数组来获取排序后的数据。注意, 最后一个键是排序的主键。
  • numpy.argmax()和numpy.argmin(): 分别返回给定轴上最大和最小元素的索引。
  • numpy.nonzero(): 返回输入数组中非零元素的索引。
  • numpy.where(): 返回满足给定条件的输入数组中元素的索引。
  • numpy.extract(): 返回满足任何条件的元素。

• 字节交换

  • numpy.ndarray.byteswap(): 在两种表示之间切换(大端和小端)。

8. 矩阵库

NumPy包包含一个矩阵库 numpy.matlib 。该模块提供了返回矩阵而不是ndarray对象的函数。

• matlib.empty(): 返回一个未初始化条目的新矩阵。
• matlib.zeros(): 返回一个填充了零的矩阵。
• matlib.ones(): 返回一个填充有1的矩阵。
• matlib.eye(): 返回一个矩阵, 对角线上的元素为1, 其他位置为0。numpy.matlib.eye(n, M,k, dtype)
• matlib.identity(): 返回给定大小的单位矩阵。单位矩阵是一个所有对角元素都为1的方阵。
• matlib.rand(): 返回一个给定大小的矩阵, 其中填充有随机值。

9. 线性代数

• numpy.dot(): 返回两个数组的点积。对于2维向量, 它等价于矩阵乘法。对于1维数组, 它是两个向量的内积。对于N维数组, 它是沿着a的最后一个轴和b的倒数第二个轴的点乘和。
  向量 a 和 b 的点积定义如下:
  
  \[ \sum^n_{i=1}(a_ib_i) \]
• numpy.vdot(): 返回两个向量的点积。如果第一个参数是复数, 那么它的共轭将用于计算。如果参数id是多维数组, 则会被压平。
• numpy.inner(): 数返回1-D数组的向量内积。对于更高的维度, 它返回最后一个轴上的点积和。

np.inner(np.array([1,2,3]),np.array([0,1,0])) 
# Equates to 1*0+2*1+3*0

• numpy.matmul(): 返回两个数组的矩阵乘积。当两个数组都是2-D数组时, 返回一个普通乘积；但如果任一参数的维度>2, 则将其视为最后两个索引中的一组矩阵, 并进行相应的广播。另一方面, 如果任一参数是1-D数组, 则通过在其维度后附加1将其升级为矩阵, 但在乘法完成后被移除。

a = np.arange(8).reshape(2,2,2) 
b = np.arange(4).reshape(2,2) 
print(np.matmul(a,b))

• numpy.linalg.solve(): 给出线性方程组在矩阵形式下的解。

10.1 Poly1d

• numpy.polyfit: 使用的是最小二乘法进行多项式拟合

# numpy.polyfit(x, y, deg, rcond=None, full=False, w=None, cov=False)
x = np.array([ 0.0, 1.0, 2.0, 3.0,  4.0,  5.0 ])
y = np.array([ 0.0, 0.8, 0.9, 0.1, - 0.8, - 1.0 ])
z = np.polyfit(x, y, 3)
print(z)

• np.poly1d: 构造多项式\(x^2 + 2x + 3\)

coff = np.array([1, 2, 3])
p = np.poly1d(coff)
print(p)

print(p(0.5))

10. 与Matplotlib结合

Matplotlib是Python的绘图库, 它与NumPy一起使用, 为MatLab提供了一个有效的开源替代方案。它也可以与PyQt和wxPython等图形工具包一起使用。
Matplotlib模块最初是由John D. Hunter编写的。自2012年以来, Michael Droettboom是主要开发者。目前, Matplotlib的稳定版本是1.5.1。该软件包可在www.matplotlib.org二进制分发和源代码形式上获得。
pyplot() 是matplotlib库中最重要的函数, 用于绘制2D数据。下面的脚本绘制了方程 y = 2x + 5:

import numpy as np 
from matplotlib import pyplot as plt 

x = np.arange(1,11) 
y = 2 * x + 5 
plt.title("Matplotlib demo") 
plt.xlabel("x axis caption") 
plt.ylabel("y axis caption") 
plt.plot(x,y) 
plt.show()

10.1 格式化字符

序号	字符和描述
1	‘-’ 实线样式
2	‘-’ 虚线样式
3	‘-.’ 点划线样式
4	‘:’ 点线样式
5	‘.’ 点标记
6	‘,’ 像素标记
7	‘o’ 圆形标记
8	‘v’ 向下三角标记
9	‘^’ 向上三角标记
10	‘<’ 三角形左标记
11	‘>’ 三角形右标记
12	‘1’ 三角形向下标记
13	‘2’ 三角形向上标记
14	‘3’ 三角形向左标记
15	‘4’ 三角形向右标记
16	’s’ 方形标记
17	‘p’ 五边形标记
18	‘*’ 星形标记
19	‘h’ 六边形1标记
20	‘H’ 六边形2标记
21	‘+’ 加号标记
22	‘x’ X标记
23	‘D’ 菱形标记
24	’d’ 细菱形标记
25	| 竖线标记
26	‘_’ 横线标记

10.2 颜色缩写定义|

Character	Color
‘b’	Blue
‘g’	Green
‘r’	Red
‘c’	Cyan
’m’	Magenta
‘y’	Yellow
‘k’	Black
‘w’	White

10.3 其他绘图函数

• subplot()函数允许您在同一图中绘制不同的内容。在下面的脚本中, 绘制了正弦和余弦值。
• bar() 函数生成条形图。
• 直方图:
  NumPy拥有一个 numpy.histogram() 函数, 用于图形化地表示数据的频率分布。每个类间隔对应的水平大小相等的矩形, 以及对应的频率的变量高度。pyplot子模块的 hist()函数 接受包含数据和bin数组的参数, 并将其转换为直

参考:
SciPy 文档：稀疏矩阵
The Rank of a Matrix
Wolfram MathWorld - Determinant
The determinant | Chapter 6, Essence of linear algebra
特征向量和特征值的图形化解释